
【题目】不等式组 ![]() 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:解2x+2>0,2x>-2,x>-1;
解-x≥-1,得x≤1,
则不等式组的解集为-1<x≤1.
在数轴上表示为:![]()
故选D.
【考点精析】认真审题,首先需要了解一元一次不等式组的解法(解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )),还要掌握在数轴上表示不等式组的解集(不等式组的解集可以在数轴上表示出来;当任何数x都不能使不等式同时成立,我们就说这个不等式组无解或其解为空集)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】观察下面算式,解答问题:
![]()
![]()
![]() ……
……
(1)请求出1 3 5 7 9 11的结果为 ;
请求出1 3 5 7 9 29 的结果为 ;
(2)若n 表示正整数,请用含 n 的代数式表示1 3 5 7 9 (2n 1) (2n 1) 的值为
(3)请用上述规律计算: 41 43 45 77 79 的值(要求写出详细解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为 ![]() O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使
O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 ![]() PED=
PED= ![]() C.
C.
(1)求证:PE是 ![]() O的切线;
O的切线;
(2)求证:ED平分 ![]() BEP;
BEP;
(3)若 ![]() O的半径为5,CF=2EF,求PD的长.
O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(A2013防城港)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
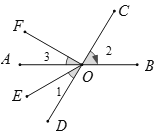
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一中学组织七年级部分学生和老师到苏州乐园开展社会实践活动,租用的客车有50座和30座两种可供选择.学校根据参加活动的师生人数计算可知:若只租用30座客车x辆,还差5人才能坐满;
(1)则该校参加此次活动的师生人数为 (用含x的代数式表示);
(2)若只租用50座客车,比只租用30座客车少用2辆,求参加此次活动的师生至少有多少人?
(3)已知租用一辆30座客车往返费用为400元,租用一辆50座客车往返费用为600元,学校根据师生人数选择了费用最低的租车方案,总费用为2200元,试求参加此次活动的师生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com