
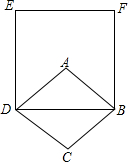
 如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48. 科目:初中数学 来源: 题型:选择题
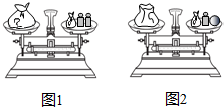 如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )
如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
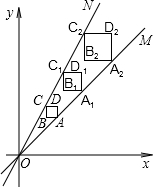 如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.
如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
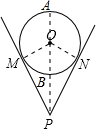 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )| A. | $\frac{50}{3}$πcm | B. | 50πcm | C. | $\frac{50}{6}$πcm | D. | 50$\sqrt{3}$πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
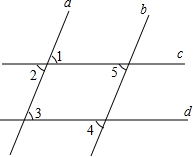 如图所示,则下列说法中不正确的是( )
如图所示,则下列说法中不正确的是( )| A. | 由a∥b能得到∠2=∠5 | B. | 由c∥d能得到∠3=∠1 | ||
| C. | 由c∥d能得到∠3=∠4 | D. | 由a∥b能得到∠1=∠5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 82元 | B. | 100元 | C. | 120元 | D. | 160元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
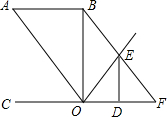 如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么?
如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com