
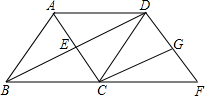
 已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形.
已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形. 分析 首先利用中位线定理证得CG∥BD,CG=$\frac{1}{2}BD$,然后根据四边形ABCD是菱形得到AC⊥BD,DE=$\frac{1}{2}BD$,从而得到∠DEC=90°,CG=DE,最后利用CG∥BD,得到四边形ECGD是矩形.
解答 证明:∵CF=BC,
∴C点是BF中点,
∵点G是DF中点,
∴CG是△DBF中位线,
∴CG∥BD,CG=$\frac{1}{2}BD$,
∵四边形ABCD是菱形,
∴AC⊥BD,DE=$\frac{1}{2}BD$,
∴∠DEC=90°,CG=DE,
∵CG∥BD,
∴四边形ECGD是矩形.
点评 本题考查了矩形的判定、菱形的性质及三角形的中位线定理,解题的关键是牢记菱形的有关判定的方法,难度不大.


科目:初中数学 来源: 题型:选择题
| 价格/(元/kg) | 12 | 10 | 8 | 合计/kg |
| 小菲购买的数量/kg | 2 | 2 | 2 | 6 |
| 小琳购买的数量/kg | 1 | 2 | 3 | 6 |
| A. | 一样划算 | B. | 小菲划算 | C. | 小琳划算 | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
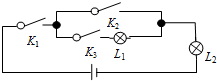 物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com