
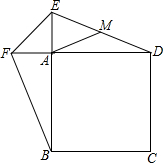
 如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由.
如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由. 分析 结论:AM=$\frac{1}{2}$BF.△ABF≌△ADE,TC BF=DE,在Rt△AED中,由EM=MD,推出AM=$\frac{1}{2}$DE,由此即可证明.
解答 解:结论:AM=$\frac{1}{2}$BF.
理由:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=∠FAB=∠EAD=90°,
在△ABF和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=}\\{AF=AE}\end{array}\right.$,
∴△ABF≌△ADE,
∴BF=DE,
在Rt△AED中,∵EM=MD,
∴AM=$\frac{1}{2}$DE,
∴AM=$\frac{1}{2}$BF.
点评 本题考查正方形的性质.全等三角形的判定和性质,直角三角形斜边中线性质等知识,解题的关键是正确寻找全等三角形解决问题,属于基础题,中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
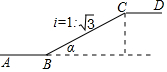 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
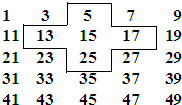 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com