
分析 先估算$\sqrt{14}$的范围,求出7+$\sqrt{14}$和7-$\sqrt{14}$的范围,求出a、b的值,最后代入求出即可.
解答 解:∵3<$\sqrt{14}$<4,
∴10<7+$\sqrt{14}$<11,-4<-$\sqrt{14}$<-3,
∴3<7-$\sqrt{14}$<4,
∴a=7+$\sqrt{14}$-10=$\sqrt{14}$-3,b=7-$\sqrt{14}$-3=4-$\sqrt{14}$,
∴(a+b)2014=[($\sqrt{14}$-3)+(4-$\sqrt{14}$)]2014=1,
故答案为:1.
点评 本题考查了估算无理数的大小,能估算出7+$\sqrt{14}$和7-$\sqrt{14}$的范围是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
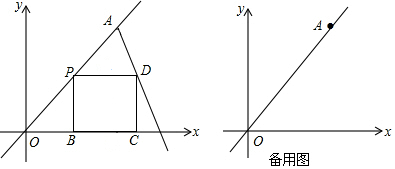
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
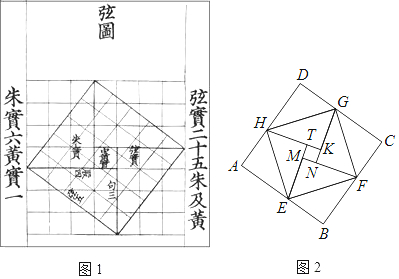
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
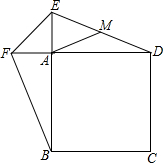 如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由.
如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
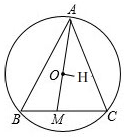 如图,锐角三角形ABC内接于半径为R的⊙O,H是三角形ABC的垂心,AO的延长线与BC交于点M,若OH⊥AO,BC=10,OA=6,则OM的长=$\frac{11}{3}$.
如图,锐角三角形ABC内接于半径为R的⊙O,H是三角形ABC的垂心,AO的延长线与BC交于点M,若OH⊥AO,BC=10,OA=6,则OM的长=$\frac{11}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
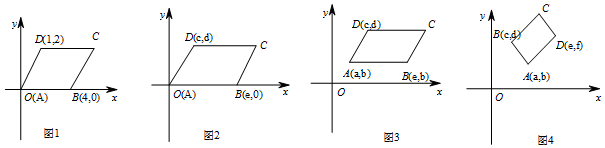
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com