
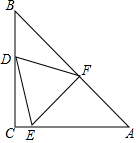
 如图,△ABC中,∠C=90°,CA=CB=3,△DEF是△ABC的内接等边三角形,且BD=$\sqrt{3}$,求BE的长.
如图,△ABC中,∠C=90°,CA=CB=3,△DEF是△ABC的内接等边三角形,且BD=$\sqrt{3}$,求BE的长. 分析 作辅助线,构建相似三角形和全等三角形,证明△BDN∽△AEM和△DNF≌△FME,由相似得:$\frac{BD}{AE}=\frac{DN}{EM}=\frac{BN}{AM}$,由全等得:DN=FM,FN=EM,根据等腰三角形BDH求DH和BH的长,利用60度角的三角函数求DN的长,从而得到NH的长,设AE=x,则EC=3-x,由比例式表示出EM和AM的长,代入AB列等式可求得x的值,最后利用勾股定理求BE的长.
解答 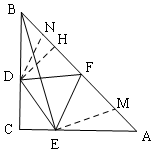 解:作∠BDN=∠AEM=15°,交AB于N、M,
解:作∠BDN=∠AEM=15°,交AB于N、M,
∵∠C=90°,CA=CB,
∴∠A=∠B=45°,
∴△BDN∽△AEM,
∴$\frac{BD}{AE}=\frac{DN}{EM}=\frac{BN}{AM}$,
∵∠DNF=45°+15°=60°=∠EMF,
∴∠FEM+∠EFM=120°,
∵△DEF是等边三角形,
∴DF=EF,∠DFE=60°,
∴∠DFN+∠EFM=120°,
∴∠FEM=∠DFN,
在△DNF和△FME中,
∵$\left\{\begin{array}{l}{∠FEM=∠DFN}\\{∠EMF=∠DNF}\\{EF=DF}\end{array}\right.$,
∴△DNF≌△FME(AAS),
∴DN=FM,FN=EM,
过D作DH⊥AB于H,
∴△DBH是等腰直角三角形,
∵BD=$\sqrt{3}$,
∴BH=DH=$\frac{\sqrt{6}}{2}$,
在Rt△DNH中,∠DNF=60°,
∴∠NDH=30°,
sin60°=$\frac{DH}{DN}$,
∴DN=$\frac{\sqrt{6}}{2}$$÷\frac{\sqrt{3}}{2}$=$\sqrt{2}$,
∴NH=$\frac{\sqrt{2}}{2}$,
∴BN=BH-NH=$\frac{\sqrt{6}}{2}$-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$,
设AE=x,则EC=3-x,
∴$\frac{\sqrt{3}}{x}=\frac{\sqrt{2}}{EM}=\frac{\frac{\sqrt{6}-\sqrt{2}}{2}}{AM}$,
∴EM=$\frac{\sqrt{2}x}{\sqrt{3}}$,AM=$\frac{\sqrt{6}-\sqrt{2}}{2\sqrt{3}}$x,
由勾股定理得:AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵AB=BN+FN+FM+AM,
∴$\frac{\sqrt{6}-\sqrt{2}}{2}$+$\frac{\sqrt{2}x}{\sqrt{3}}$+$\sqrt{2}$+$\frac{\sqrt{6}-\sqrt{2}}{2\sqrt{3}}$x=3$\sqrt{2}$,
解得:x=9-4$\sqrt{3}$,
∴AE=9-4$\sqrt{3}$,
∴EC=3-(9-4$\sqrt{3}$)=4$\sqrt{3}$-6,
在Rt△BEC中,由勾股定理得:BE=$\sqrt{{3}^{2}+(4\sqrt{3}-6)^{2}}$=$\sqrt{93-48\sqrt{3}}$.
点评 本题考查了等腰直角三角形的性质、等边三角形的性质、相似三角形和全等三角形的性质和判定、三角函数和勾股定理,作辅助线构建相似三角形和全等三角形是本题的关键;有难度,计算量大.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
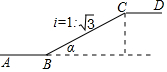 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:$\sqrt{3}$,则电梯坡面BC的坡角α为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com