
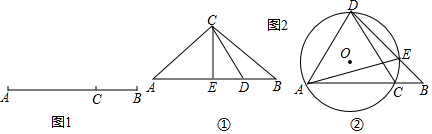
分析 (1)设AC=x,根据和谐点的定义求出x,即可解决问题.
(2)①是真命题.根据和谐点的定义证明即可.②是假命题.根据和谐点的定义证明即可.
(3)如图②中,作DQ⊥AB于Q,FH⊥AD于H.设BC=y,由点C是线段AB的和谐点,可得$\frac{m}{m+x}$=$\frac{2x}{m}$,解得x=$\frac{\sqrt{3}-1}{2}$m,由△ABC是等边三角形,边长为m,由DQ⊥AC,DQ=$\frac{\sqrt{3}}{2}$m,AQ=QC=$\frac{1}{2}$m,∠DAC=∠ACD=∠ADC=∠DEA=60°,推出QD=QB,推出∠B=45°,再证明∠DAF=45°,即可解决问题.
解答 解:(1)设AC=x,
∵点C是线段AB的和谐点,
∴$\frac{x}{1}$=2×$\frac{1-x}{x}$,
整理得x2+2x-2=0,
解得x=-1+$\sqrt{3}$或-1-$\sqrt{3}$(舍弃),
∴AC=$\sqrt{3}$-1,$\frac{AC}{AB}$=$\sqrt{3}$-1.
(2)①是真命题.
理由:如图①中,设AE=a,
∵CE⊥AD,∠A=45°,∠ADC=60°,
∴∠ACE=∠A=45°,∠ECD=30°,
∴AE=EC=a,ED=BD=$\frac{\sqrt{3}}{3}$a,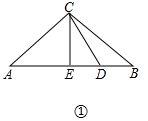
∴$\frac{AD}{AB}$=$\frac{a+\frac{\sqrt{3}}{3}a}{a+\frac{2\sqrt{3}}{3}a}$=$\sqrt{3}$-1,2×$\frac{DB}{AD}$=$\frac{2×\frac{\sqrt{3}}{3}a}{a+\frac{\sqrt{3}}{3}}$=$\sqrt{3}$-1,
∴$\frac{AD}{AB}$=2×$\frac{BD}{AD}$,
∴点D是线段AB的和谐点.
②是假命题.
理由:如图①中,
由①可知:$\frac{AE}{AD}$=$\frac{a}{a+\frac{\sqrt{3}}{3}a}$=$\frac{3-\sqrt{3}}{2}$,2×$\frac{ED}{AE}$=$\frac{2×\frac{\sqrt{3}}{3}a}{a}$=$\frac{2\sqrt{3}}{3}$,
∴$\frac{AE}{AD}$≠2×$\frac{ED}{AE}$,
∴点E不是线段AD的和谐点.
(3)如图②中,作DQ⊥AB于Q,FH⊥AD于H.设BC=y,
∵点C是线段AB的和谐点,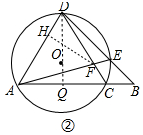
∴$\frac{m}{m+x}$=$\frac{2x}{m}$,
整理得,2x2+2mx-m2=0,
解得x=$\frac{\sqrt{3}-1}{2}$m或$\frac{-\sqrt{3}-1}{2}$m(舍弃),
∵△ABC是等边三角形,边长为m,DQ⊥AC,
∴DQ=$\frac{\sqrt{3}}{2}$m,AQ=QC=$\frac{1}{2}$m,∠DAC=∠ACD=∠ADC=∠DEA=60°,
∵BC=$\frac{\sqrt{3}-1}{2}$m,
∴QB=QC+BC=$\frac{\sqrt{3}}{2}$m,
∴QD=QB,
∴∠B=45°,
∵∠DEA=∠B+∠EAB=60°,
∴∠EAB=15°,
∴∠DAE=45°
∵FH⊥AD,
∴∠HAF=∠HFA=45°,
∴AH=HF,
在Rt△DHF中,设DH=y,∵∠DHF=30°,
∴DF=2DH=2y,FH=AH=$\sqrt{3}$y,
∵AD=m,
∴y+$\sqrt{3}$y=m,
∴y=$\frac{m}{\sqrt{3}+1}$,
∴DF=2y=$\frac{2m}{\sqrt{3}+1}$=($\sqrt{3}$-1)m.
点评 本题考查圆综合题、等边三角形的性质、等腰直角三角形的判定和性质、分式方程、和谐点的定义等知识,解题的关键是学会理解题意,学会构建方程解决问题,第三个问题的突破点是证明DQ=QB,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
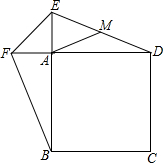 如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由.
如图,正方形ABCD,E,F分别在BA、DA的延长线上,且AE=AF,连接EF,BF,DE,点M是DE的中点,连接AM,判断AM与BF之间的数量关系,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
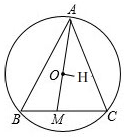 如图,锐角三角形ABC内接于半径为R的⊙O,H是三角形ABC的垂心,AO的延长线与BC交于点M,若OH⊥AO,BC=10,OA=6,则OM的长=$\frac{11}{3}$.
如图,锐角三角形ABC内接于半径为R的⊙O,H是三角形ABC的垂心,AO的延长线与BC交于点M,若OH⊥AO,BC=10,OA=6,则OM的长=$\frac{11}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
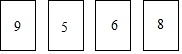 康康家购置了一辆新车,爸爸妈妈商议确定车牌号,前四位选定为鲁DF32后,对后两位数字意见有分歧,最后决定由毫不知情的康康从如图排列的四个数字中随机划去两个,剩下的两个数字从左到右组成两位数,续在DF32之后,则选中的车牌号为DF3258的概率是$\frac{1}{6}$.
康康家购置了一辆新车,爸爸妈妈商议确定车牌号,前四位选定为鲁DF32后,对后两位数字意见有分歧,最后决定由毫不知情的康康从如图排列的四个数字中随机划去两个,剩下的两个数字从左到右组成两位数,续在DF32之后,则选中的车牌号为DF3258的概率是$\frac{1}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
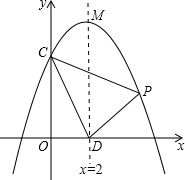 如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com