
 如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.
如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.分析 (1)先根据OC是∠AOB的平分线得出OC的解析式为y=x.再利用待定系数法求出直线AB的解析式,故可得出C点坐标,用t表示出点M与点N的坐标,再由轴对称的性质可得出P、Q两点的坐标;
(2)①分CP=PQ,PQ=QC及CP=CQ三种情况进行讨论即可;
②当0<t≤1时,S=S△POC+S△OQC-S△OPQ,当1<t<2时,设PQ与AB交于点D,则重叠部分面积为△CDQ的面积,据此可得出结论.
解答 解:(1)∵OC是∠AOB的平分线,
∴OC的解析式为y=x.
设直线AB的解析式为y=kx+b(k≠0),
∵点A(4,0)、B(0,2),
∴$\left\{\begin{array}{l}0=4k+b\\ b=2\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=2\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{1}{2}$x+2,
∴$\left\{\begin{array}{l}y=x\\ y=-\frac{1}{2}x+2\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{4}{3}\\ y=\frac{4}{3}\end{array}\right.$,
∴C($\frac{4}{3}$,$\frac{4}{3}$).
∵动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,
∴M(2t,0),N(0,t).
∵点P、Q为点M、N关于直线OC的对称点,
∴P(0,2t),Q(t,0);
(2)①当CP=PQ,∠CPQ=90°时,此种情况不存在;
当PQ=QC,∠PQC=90°时,此种情况不存在;
当CP=CQ,∠PCQ=90°时,如图1,
∵P(0,2t),Q(t,0),C($\frac{4}{3}$,$\frac{4}{3}$),
∴2t-$\frac{4}{3}$=$\frac{4}{3}$-t,解得t=$\frac{8}{9}$;
②如图1,当0<t≤1时,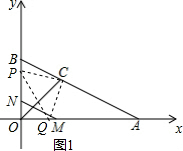
S=S△POC+S△OQC-S△OPQ
=$\frac{1}{2}$×$\frac{4}{3}$×2t+$\frac{1}{2}$t×$\frac{4}{3}$-$\frac{1}{2}$t×2t
=-t2+2t;
如图2所示,当1<t<2时,设PQ与AB交于点D,则重叠部分面积为△CDQ的面积.
设直线PQ的解析式为y=kx+b(k≠0),
∵P(0,2t),Q(t,0),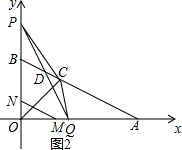
∴$\left\{\begin{array}{l}b=2t\\ kt+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}k=-2\\ b=2t\end{array}\right.$,
∴直线PQ的解析式为y=-2x+2t.
∵直线AB的解析式为y=-$\frac{1}{2}$x+2,
∴$\left\{\begin{array}{l}y=-2x+2t\\ y=-\frac{1}{2}x+2\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{4}{3}t-\frac{4}{3}\\ y=-\frac{2}{3}t+\frac{8}{3}\end{array}\right.$,
∴D($\frac{4}{3}$t-$\frac{4}{3}$,-$\frac{2}{3}$t+$\frac{8}{3}$),
∴S=S△AQD-S△AQC
=$\frac{1}{2}$(4-t)•(-$\frac{2}{3}$t+$\frac{8}{3}$)-$\frac{1}{2}$(4-t)×$\frac{4}{3}$
=$\frac{1}{3}$t2-2t+$\frac{8}{3}$.
综上所述,S=$\left\{\begin{array}{l}-{t}^{2}+2t(0<t≤1)\\ \frac{1}{3}{t}^{2}-2t+\frac{8}{3}(1<t<2)\end{array}\right.$.
点评 本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式、图形面积的计算的知识,在解答(2)时要注意进行分类讨论.


科目:初中数学 来源: 题型:选择题
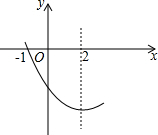 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ③④⑤ | C. | ②④⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某矿泉水厂生产一种矿泉水,经侧算,用一吨水生产的矿泉水所获利润y(元)与1吨水的价格x(元)的关系如图所示.
某矿泉水厂生产一种矿泉水,经侧算,用一吨水生产的矿泉水所获利润y(元)与1吨水的价格x(元)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
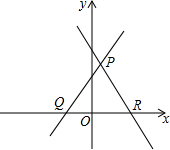 对于平面直角坐标系中相交的两条直线,给出如下定义:若相交的两条直线分别与x轴相交所构成的两锐角相等,则称这两条直线为“泛对称直线”.例如在图中,若∠PQR=∠PRQ,则直线PQ与直线PR称为“泛对称直线”;反之,若直线PQ与直线PR是“泛对称直线”,则有∠PQR=∠PRQ.解答下列问题.
对于平面直角坐标系中相交的两条直线,给出如下定义:若相交的两条直线分别与x轴相交所构成的两锐角相等,则称这两条直线为“泛对称直线”.例如在图中,若∠PQR=∠PRQ,则直线PQ与直线PR称为“泛对称直线”;反之,若直线PQ与直线PR是“泛对称直线”,则有∠PQR=∠PRQ.解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com