
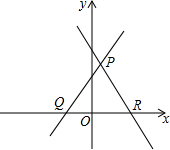
 对于平面直角坐标系中相交的两条直线,给出如下定义:若相交的两条直线分别与x轴相交所构成的两锐角相等,则称这两条直线为“泛对称直线”.例如在图中,若∠PQR=∠PRQ,则直线PQ与直线PR称为“泛对称直线”;反之,若直线PQ与直线PR是“泛对称直线”,则有∠PQR=∠PRQ.解答下列问题.
对于平面直角坐标系中相交的两条直线,给出如下定义:若相交的两条直线分别与x轴相交所构成的两锐角相等,则称这两条直线为“泛对称直线”.例如在图中,若∠PQR=∠PRQ,则直线PQ与直线PR称为“泛对称直线”;反之,若直线PQ与直线PR是“泛对称直线”,则有∠PQR=∠PRQ.解答下列问题.分析 (1)①利用“泛对称直线”的定义判断即可;②利用“泛对称直线”的定义k1与k2,b1与b2的关系即可;
(2)利用“泛对称直线”的定义找出过A点直线的斜率,根据OA的长确定出A的坐标,即可确定出所求直线解析式.
解答 解:(1)①同一平面直角坐标系中两直线l1:y=x+3与直线l2:y=-x+3一定是“泛对称直线”.(√)
②若同一平面直角坐标系中两条相交的直线y=k1x+b1(k1≠0)与y=k2x+b2(k2≠0)是“泛对称直线”,则必有k1+k2=0,b1=b2.(×);
故答案为:①√;②×;
(2)∵经过A点且与直线l2:y=2x+4是“泛对称直线”,
∴两直线斜率之和为0,即过A点且与直线l2:y=2x+4是“泛对称直线”的直线斜率为-2,
设为y=-2x+b,
把(0,2)代入得:b=2,
则所求直线解析式为y=-2x+2.
点评 此题属于一次函数综合题,涉及的知识有:一次函数的图象与性质,坐标与图形性质,弄清题中“泛对称直线”的定义是解本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,AB=AC,DB⊥AB,DC⊥AC,若E、F、G、H分别是各边的中点.
如图,AB=AC,DB⊥AB,DC⊥AC,若E、F、G、H分别是各边的中点. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.
如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2008 | B. | 2009 | C. | 2014 | D. | 2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com