
分析 (1)根据有理化因式的定义,仿照阅读中例子,得到$\sqrt{3}$、$\sqrt{2}$+1的有理化因式;
(2)利用分式的基本性质,分子和分母都乘以各自分母的有理化因式,化去分母中的根号.
解答 解:(1)因为$\sqrt{3}$×$\sqrt{3}$=3,所以$\sqrt{3}$的有理化因式是$\sqrt{3}$;
因为($\sqrt{2}+1$)($\sqrt{2}$-1)=3,所以$\sqrt{2}+1$的有理化因式是$\sqrt{2}$-1
故答案为:$\sqrt{3}$,$\sqrt{2}-1$
(2)$\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
$\frac{3}{3+\sqrt{6}}=\frac{3(3-\sqrt{6})}{(3+\sqrt{6})(3-\sqrt{6})}$
=3-$\sqrt{6}$
故答案为:$\frac{2\sqrt{5}}{5}$,3-$\sqrt{6}$
点评 本题考查了分母有理化的定义以及如何利用有理化因式化去分母中的根号.一般来说,$\sqrt{a}$,b$\sqrt{a}$,($\sqrt{a}$$+\sqrt{b}$)的有理化因式分别是$\sqrt{a}$,$\sqrt{a}$,($\sqrt{a}$$-\sqrt{b}$).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:填空题
关于x的一元二次方程(m-1)x2+x+m2-1=0的一个根为0,则m的值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
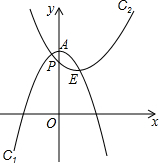 如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).
如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
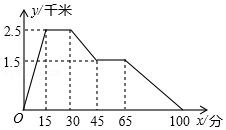 如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题:
如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com