
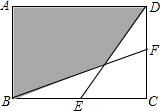
 如图,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是32 cm2.
如图,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是32 cm2. 分析 连接BD,EF,可看出阴影部分的面积等于$\frac{1}{2}$正方形的面积+一个三角形DGB的面积,用相似求出三角形的面积,阴影部分的面积可证.
解答 解:连接BD,EF.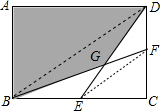
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD=6cm,AD=BC=8cm,
∴△ABD的面积=$\frac{1}{2}$正方形ABCD的面积=$\frac{1}{2}$×6×8=24(cm2),
阴影部分的面积=△ABD的面积+△BDG的面积 (G为BF与DE的交点),
∵△BCD中EF为中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴△GEF∽△GDB,
∴DG=2GE,
∴△BDE的面积=$\frac{1}{2}$△BCD的面积.
∴△BDG的面积=$\frac{2}{3}$△BDE的面积=$\frac{1}{3}$△BCD的面积=$\frac{1}{3}$×24cm2=8cm2,
∴阴影部分的面积=24cm2+8cm2=32cm2,
故答案为32.
点评 本题考查正方形的性质,三角形的面积,中位线性质的应用,注意正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知圆O,
已知圆O,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com