
分析 (1)根据余油量=原有油量-用油量,可得出余油量Q(升)与耕地时间t(时)之间的函数关系式;
(2)利用耕地时间t≥0,用油量不能超过原有油量得出自变量t的取值范围;
(3)将t=4小时30分钟后代入(1)所求的关系式,可求油箱内还有多少油.
解答 解:(1)原有油量=56升,用油量=6t,
由题意得:Q=56-6t;
(2)由题意,得6t≤56,
解得:t≤$\frac{28}{3}$,
又∵t≥0,
∴0≤t≤$\frac{28}{3}$,
所以自变量t的取值范围是0≤t≤$\frac{28}{3}$;
(3)将t=4.5代入Q=56-6t,得Q=56-6×4.5=29(升).
点评 本题考查了一次函数的应用,根据余油量=原有油量-用油量得出Q与t的关系式是解答本题的关键,要注意将实际问题与函数中的未知数联系一起.


科目:初中数学 来源: 题型:解答题
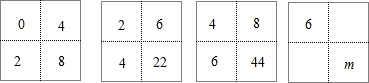
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
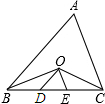 已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.
已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
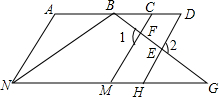 如图,∠1=∠2,∠D=∠CMG.
如图,∠1=∠2,∠D=∠CMG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,大正方形由9个相同的小正方形组成,其中三个小正方形已经涂黑,如果从其余6个小正方形中再任意选一个也涂黑,那么整个大正方形中涂黑部分成为轴对称图形的概率是$\frac{2}{3}$.
如图,大正方形由9个相同的小正方形组成,其中三个小正方形已经涂黑,如果从其余6个小正方形中再任意选一个也涂黑,那么整个大正方形中涂黑部分成为轴对称图形的概率是$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
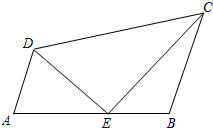 如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.
如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com