
【题目】如图,BD是∠ABC的角平分线,DE∥BC,交AB于点E,∠A=45°, ∠BDC=60°。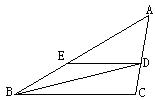
(1)求∠C的度数;
(2)求∠BED的度数.
【答案】
(1)
解:∵∠A=45°,∠BDC=60°,
∴∠ABD=∠BDC-∠A=15°.
∵BD是△ABC的角平分线,
∴∠DBC=∠ABD=15°,
∴∠ABC=30°,
∠C=180°-∠A-∠ABC=105°
(2)
∵DE∥BC,
∴∠AED=∠ABC=30°,
∠BED=180°-30°=150°
【解析】先根据三角形外角的性质求∠ABD,再根据角平分线的定义,可得∠DBC=∠ABD,利用三角形的内角和为180°求出∠C的度数;运用平行线的性质得∠BDE的度数,进而得出结论.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则: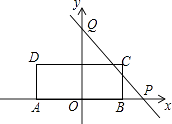
(1)a的取值范围是;
(2)若设直线PQ为:y=kx+2(k≠0),则此时k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC
(1)如图1,若α+β= ![]() ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某印刷厂印刷某尺寸的广告纸,印刷张数为a(单位:万张),需按整千张印刷计费,收费规定如下: ①若a≤1:单价为0.4元/张;
②若1<a≤2:每增加0.1万张,所有广告纸每张减少0.01元,费用再9折优惠;
③若a>2:每增加0.1万张,所有广告纸每张减少0.02元,费用再8折优惠.
(1)若某客户要印刷广告纸1.5万张,则该客户需支付费用元;
(2)若某客户支付了广告纸费用0.6万元,求印刷张数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(﹣2,3)向右平移a个单位长度,再向下平移b个单位长度,平移后对应的点为A′,且点A和A′关于原点对称,则a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图: 
(1)在甲图中,画出一个平行四边形A1B1C1D1 , 使其面积为3;
(2)在乙图中,画出一个正方形A2B2C2D2 , 使其面积为5;
(3)在丙图中,画出一个菱形A3B3C3D3 , 使其面积为6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C , 连结AC并延长到D , 使CD=CA , 连结BC并延长到E , 使CE=CB , 连结DE , A、B的距离为( )
A.线段AC的长度
B.线段BC的长度
C.线段DE长度
D.无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com