
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则: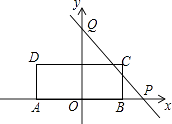
(1)a的取值范围是;
(2)若设直线PQ为:y=kx+2(k≠0),则此时k的取值范围是 .
【答案】
(1)﹣2≤a≤2
(2)k≤﹣1或k≥1
【解析】解:(1)连接QC延长与x轴相交于P1 , 根据中位线定理可知OP1=2,
连接QD延长与x轴交于点P2 , 则OP2=2,
所以实数a的取值范围是﹣2≤a≤2.
所以答案是:﹣2≤a≤2.(2)如图,当点P位于点P1处时,由(1)知P1(2,0),则0=2k+2,解得k=﹣1;
当点点P位于点P2处时,由(1)知P2(﹣2,0),则0=﹣2k+2,解得k=1;
则k的取值范围是k≤﹣1或k≥1.
故答案是:k≤﹣1或k≥1.
【考点精析】掌握一次函数的图象和性质是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
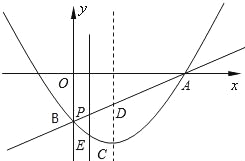
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com