
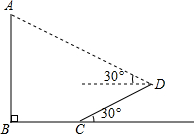
 已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知
已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知| 3 |
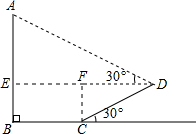 解:过D作DE⊥AB,CF⊥DE,可得EF=BC=3米,BE=CF,
解:过D作DE⊥AB,CF⊥DE,可得EF=BC=3米,BE=CF,| 1 |
| 2 |
| CD2-CF2 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |


科目:初中数学 来源: 题型:
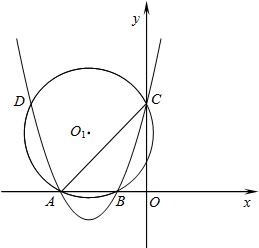 抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300
热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
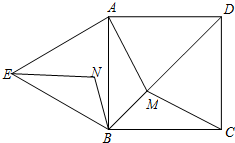 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com