
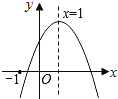
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的个数有( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
①观察函数图象发现:抛物线的开口向下,对称轴为x=1,抛物线与y轴的交点在y轴正半轴,由此即可得出a<0,b=-2a>0,c>0,从而得出abc<0,结论①不符合题意;②由当x=-1时,y<0可知a-b+c>0,变形后可得出b>a+c,结论②符合题意;③由抛物线的对称轴为x=1,可知x=0与x=2时,y值相等,结合抛物线与y轴交点在y轴正半轴即可得出4a+2b+c=c>0,结论③符合题意;④由抛物线与x轴有两个不同的交点即可得出一元二次方程ax2+bx+c=0有两个不相等的实数根,利用根的判别式即可得出△=b2-4ac>0,结论④符合题意.综上即可得出结论.
解:①∵抛物线的开口向下,对称轴为x=1,抛物线与y轴的交点在y轴正半轴,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,结论①不符合题意;
,结论①不符合题意;
②∵当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,结论②符合题意;
,结论②符合题意;
③∵抛物线的对称轴为x=1,
∴当x=0与x=2时,y值相等.
∵抛物线与y轴的交点在y轴正半轴,
∴4a+2b+c=c>0,结论③符合题意;
④∵抛物线与x轴有两个不相等的实数根,
∴一元二次方程![]() 有两个不相等的实数根,
有两个不相等的实数根,
∴![]() ,结论④符合题意.
,结论④符合题意.
故选:C.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() .与
.与![]() 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,![]() ,
,![]() ,点A,C在直线
,点A,C在直线![]() 上.
上.
(1)求点C的坐标;
(2)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(3)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线![]() 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线______;
(2)当AB=2时,求抛物线M的函数表达式以及顶点D的坐标;
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3<4),若当-2≤n≤-1时,总有x1-x3<x3-x2<0,请结合函数的图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
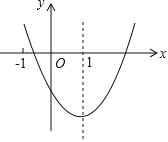
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.小正方形的顶点称为格点![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
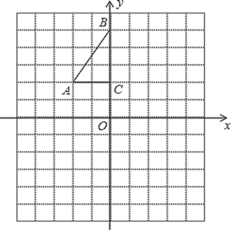
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到
,得到![]() ,请画出的图形
,请画出的图形![]() ;
;
(2)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 坐标为
坐标为![]() ,请画出平移后对应的
,请画出平移后对应的![]() ;
;
(3)若将![]() 绕某一点旋转可得到
绕某一点旋转可得到![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(4)请画出一个以![]() 为对角线,面积是20的菱形
为对角线,面积是20的菱形![]() (要求
(要求![]() ,
,![]() 是格点).
是格点).
查看答案和解析>>
科目:初中数学 来源: 题型:
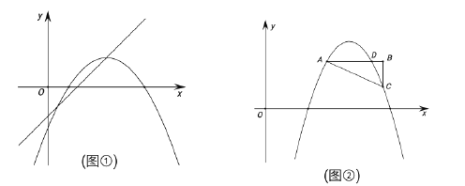
【题目】如图①,将抛物线![]() 平移到顶点恰好落在直线
平移到顶点恰好落在直线![]() 上,并设此时抛物线顶点的横坐标为
上,并设此时抛物线顶点的横坐标为![]() .
.
(1)求抛物线的解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图②,![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() ,
,![]() 轴,
轴,![]() ,
,![]() .
.
①求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
②若![]() 的面积为1,当
的面积为1,当![]() 时,
时,![]() 的最大值为-3,求
的最大值为-3,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com