
【题目】根据图(1)所示的程序,得到了y与x的函数图象如图(2),过y轴上一点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:①当x<0时,y=![]() ;②△OPQ的面积为定值;③当x>0时,y的值随x值的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的结论是( )
;②△OPQ的面积为定值;③当x>0时,y的值随x值的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的结论是( )
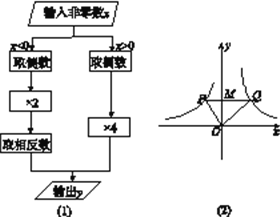
A. ①②④ B. ②④⑤ C. ③④⑤ D. ②③⑤
【答案】B
【解析】根据题意得到当x<0时,y=-![]() ,当x>0时,y=
,当x>0时,y=![]() ,设P(a,b),Q(c,d),求出ab=-2,cd=4,求出△OPQ的面积是3;x>0时,y随x的增大而减小;由ab=-2,cd=4得到MQ=2PM;因为∠POQ=90°也行,根据结论即可判断答案.
,设P(a,b),Q(c,d),求出ab=-2,cd=4,求出△OPQ的面积是3;x>0时,y随x的增大而减小;由ab=-2,cd=4得到MQ=2PM;因为∠POQ=90°也行,根据结论即可判断答案.
①、x<0,y=-![]() ,∴故此选项①错误;
,∴故此选项①错误;
②、当x<0时,y=-![]() , 当x>0时,y=
, 当x>0时,y=![]() ,
,
设P(a,b),Q(c,d),
则ab=-2,cd=4,
∴△OPQ的面积是 ![]() (-a)b+
(-a)b+![]() cd=3, ∴故此选项②正确;
cd=3, ∴故此选项②正确;
③、x>0时,y=![]() , y随x的增大而减小,故此选项③错误;
, y随x的增大而减小,故此选项③错误;
④、∵ab=-2,cd=4,∴故此选项④正确;
⑤设PM=-a,则OM=-![]() ,则PO2=PM2+OM2=(-a)2+(-
,则PO2=PM2+OM2=(-a)2+(- ![]() )2=(-a)2+
)2=(-a)2+![]() , QO2=MQ2+OM2=(-2a)2+(-
, QO2=MQ2+OM2=(-2a)2+(- ![]() a)2=4a2+ 4a2,
a)2=4a2+ 4a2,
当PQ2=PO2+QO2=(-a)2+ ![]() +4a2+
+4a2+ ![]() =5a2+
=5a2+![]() =9a2 ,
=9a2 ,
整理得:![]() =4a2 ,
=4a2 ,
∴a4=2 ,
∵a有解,
∴∠POQ=90°可能存在,故此选项⑤正确;
正确的有②④⑤,
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲玛雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“●”、划“__________”、卵形“![]() ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
(1)玛雅符号![]() 表示的自然数是__________;
表示的自然数是__________;
(2)请你在右边的方框中画出表示自然数280的玛雅符号:![]()
自然数 | 1 | 2 | 3 | 4 | 5 |
玛雅符号 | ● | ●● | ●●● | ●●●● | _______ |
自然数 | 6 | 7 | 8 | 9 | 10 |
玛雅符号 |
|
|
|
|
|
自然数 | 11 | 12 | … | 15 | 16 |
玛雅符号 |
|
| … |
|
|
自然数 | … | 19 | 20 | … | 100 |
玛雅符号 | … |
|
| … |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
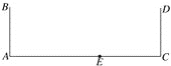
(1)在图中画出杨老师的位置(用线段FG表示),并画出光线,标明(太阳光、灯光);
(2)若上午上学时候高1米的木棒的影子为2米,杨老师身高为1.5米,他离里程碑E恰5米,求路灯高.
查看答案和解析>>
科目:初中数学 来源: 题型:
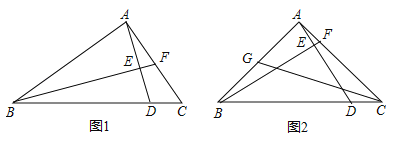
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江苏省连云港市)环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,(1)若甲单独完成需要多少天?(2)从节省资金的角度考虑,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请利用直尺和圆规完成以下问题. (要求:保留作图痕迹,补全作法)如图:在直线MN上求作一点P,使点P到射线OA和OB的距离相等.
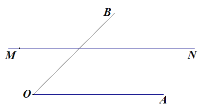
作法:(1) 以点O为圆心,适当长为半径 ,交OA于点C,交OB于点D.
(2) 分别以点C、D为圆心, ![]() CD的长为 画弧,两弧在∠AOB的 相交于点Q.
CD的长为 画弧,两弧在∠AOB的 相交于点Q.
(3) 画射线OQ,射线OQ与直线MN相交于点P,P点即为所求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com