
【题目】关于x的二次函数![]() ,其中
,其中![]() 为锐角,则:
为锐角,则:
① 当![]() 为30°时,函数有最小值-
为30°时,函数有最小值-![]() ;② 函数图象与坐标轴必有三个交点. ③ 当
;② 函数图象与坐标轴必有三个交点. ③ 当![]() <60°时,函数在x >1时,y随 x的增大而增大;④ 无论锐角
<60°时,函数在x >1时,y随 x的增大而增大;④ 无论锐角![]() 怎么变化,函数图象必过定点。其中正确的结论有( )
怎么变化,函数图象必过定点。其中正确的结论有( )
A. ①③④ B. ①④ C. ②③ D. ①②④
【答案】D
【解析】试题解析:①当a=30°时,sina=![]() ,二次函数解析式可写作:y=x2-
,二次函数解析式可写作:y=x2-![]() x=(x-
x=(x-![]() )2-
)2-![]() ;
;
所以当a为30°时,函数的最小值为-![]() ;故①正确;
;故①正确;
②令y=0,则有:2sinax2-(4sina+![]() )x-sina+
)x-sina+![]() =0,
=0,
△=(4sina+![]() )2-4×2sina×(-sina+
)2-4×2sina×(-sina+![]() )=24sin2a+
)=24sin2a+![]() >0,
>0,
所以抛物线与x轴一定有两个交点,再加上抛物线与y轴的交点,即与坐标轴有三个交点,②正确;
③∵2sina>0,且对称轴x=-![]() =1+
=1+![]() >1,
>1,
∴x=1在抛物线对称轴的左侧,因此 x>1时,y随x的增大先减小后增大;故③错误.
④y=2sinax2-(4sina+![]() )x-sina+
)x-sina+![]() =sina(2x2-4x-1)-
=sina(2x2-4x-1)-![]() x+
x+![]() ;
;
当2x2-4x-1=0,即 x=1±![]() 时,抛物线经过定点,故④正确.
时,抛物线经过定点,故④正确.
故选D.


科目:初中数学 来源: 题型:
【题目】要使多项式(x2+px+2)(x﹣q)不含关于x的二次项,则p与q的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 乘积为﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计) 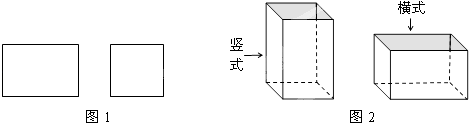
(1)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(-3,0),B(0, ![]() ),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
(1)求点C、点D的坐标并用尺规作图确定两点位置(保留作图痕迹)
(2)若半径为1的⊙P从点A出发,沿A—D—B—C以每秒4个单位长的速度匀速移动,同时⊙P的半径以每秒0.5个单位长的速度增加,运动到点C时运动停止,当运动时间为t秒时
①t为何值时,⊙P与y轴相切?
②在整个运动过程中⊙P与y轴有公共点的时间共有几秒?简述过程.
(3)若线段AB绕点O顺时针旋转90°,线段AB扫过的面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com