
����Ŀ����֪��b����С������������a��b����![]() ����ش����⣺
����ش����⣺
��1����ֱ��д��a��b��c��ֵ�� a=______�� b=________�� c=________��
��2��a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB���Լ����ʱBC��AB��ֵ��
![]()
��3���ڣ�1����2���������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��3����λ���Ⱥ�x��x>3������λ���ȵ��ٶ������˶������ʣ��Ƿ����x��ʹBC��AB��ֵ����ʱ��t�ı仯�����䣬���������x����������˵�����ɣ�
���𰸡�(1)a=-1��b=1��c=4�� (2)1�� (3)x=7
��������
��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ����ĺ���0����ÿ������0���������a��b��c��ֵ��
��2�����������ľ��빫ʽ����BC��AB��ֵ����һ���õ�BC-AB��ֵ��
��3�������BC=4t+3��AB=4t+2���Ӷ��ó�BC-AB���Ӷ���⣮
�⣺��1����b����С����������
��b=1��
��|c-4|+��a+b��2=0��
��c-4=0��a+b=0����a=-1��c=4��
��2��BC-AB
=��4-1��-��1+1��
=3-2
=1��
�ʴ�ʱBC-AB��ֵ��1��
��3��t��ʱ����A��Ӧ����Ϊ-1-t����B��Ӧ����Ϊ3t+1����C��Ӧ����Ϊxt+4��
��BC=��xt+4��-��3t+1��=(x-3)t+3��AB=��3t+1��-��-1-t��=4t+2��
��BC-AB=(x-3)t+3-��4t+2��=��x-7��t+1��
��BC-AB��ֵ������ʱ��t�ı仯���ı�ʱ����ֵΪ7��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ѧϰ��һ����������������ƽ��3����λ��������ƽ��![]() ����λ���൱������ƽ��1����λ����ʵ���ӷ���ʾΪ
����λ���൱������ƽ��1����λ����ʵ���ӷ���ʾΪ ![]() ��
��
������ƽ���ϵĵ�������ƽ�ƣ���![]() �᷽��ƽ�Ƶ�����Ϊ
�᷽��ƽ�Ƶ�����Ϊ![]() ������Ϊ��������Ϊ����ƽ��
������Ϊ��������Ϊ����ƽ��![]() ����λ������
����λ������![]() �᷽��ƽ�Ƶ�����Ϊ
�᷽��ƽ�Ƶ�����Ϊ![]() ������Ϊ��������Ϊ����ƽ��
������Ϊ��������Ϊ����ƽ��![]() ����λ���������������{
������������������{![]() ��
��![]() }������һƽ�Ƶġ�ƽ����������ƽ������{
}������һƽ�Ƶġ�ƽ����������ƽ������{![]() ��
��![]() }�롰ƽ������{
}�롰ƽ������{![]() ��
��![]() }�ļӷ����㷨��Ϊ
}�ļӷ����㷨��Ϊ![]() ��
��
������⣺��1�����㣺{3��1}+{1��2}��{1��2}+{3��1}��
��2��������P������ԭ��O�������Ȱ��ա�ƽ������{3��1}ƽ�Ƶ�A���ٰ��ա�ƽ������{1��2}ƽ�Ƶ�B�����ȰѶ���P���ա�ƽ������{1��2}ƽ�Ƶ�C���ٰ��ա�ƽ������{3��1}ƽ�ƣ�����λ�û��ǵ�B����ͼ�л����ı���OABC.
��֤���ı���OABC��ƽ���ı���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������6��3��4��7��6��3��5��6����
��1���������ݵ�ƽ��������������λ����
��2���������ݵķ���ͱ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5��23��24�գ������о��꼶ѧ���������п��������ԣ�ijУ��ȡ�˲���ѧ����һ�����������Գɼ��������Գɼ�������������ͳ��ͼ����ͬѧ�����ǰ�����Ƶ�ʺ���0��12����ͬѧ�������һ���Ƶ��Ϊ0.04����ͬѧ������������ҵڶ������������Ƶ����Ϊ4��17��15�����ͳ��ͼ�ش��������⣺
(1)��ι���ȡ�˶�����ѧ����һ�����������Գɼ���
(2)����������������130��Ϊ���㣬����β��Գɼ����������Ƕ��٣�
(3)�����β��Գɼ��е���λ����120�Σ���ô��β����У��ɼ�Ϊ120�ε�ѧ�������ж����ˣ�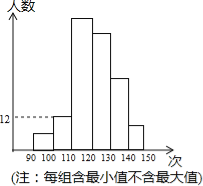
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ABCD �У�B 60 ��M ��N �ֱ�Ϊ�߶� AB ��BC �ϵ����㣬�� BM CN �� AN ��CM �ཻ�ڵ� E ��
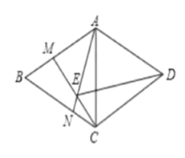
��1��֤���� BCM �� CAN ��
��2����AEM �Ķ�����
��3��֤���� AE CE DE ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ҵ����������һ�վ������������Ϊ������Σ��ֱ���50Ԫ��100Ԫ��150Ԫ��200Ԫ��300Ԫ������С�������ȡ���־��ְ����ͳ�������ǵľ������Ƴ�������������ͳ��ͼ������ͼ���е���Ϣ����������⣺
��1������С���ȡ�ľ������Ϊ_____�ˣ��벹ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�У���100Ԫ����Ӧ���ε�Բ�ĽǵĶ�����
��3����֪����ҵ����500�˲��뱾�ξ�������ƾ���ܶ��ԼΪ����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
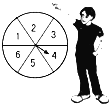
����Ŀ����ͼ��ʾ��ת�̱��ȷֳ��������Σ���������һ��д������1��2��3��4��5��6��������ת��ת�̣�����ֹͣת��ʱ����
��1��ָ��ָ��4�ĸ��ʣ�
��2��ָ��ָ�������������ĸ��ʣ�
��3��ָ��ָ�����ֲ�С��5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϲ�����й����⣺
����֪����|x|��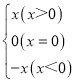 ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1��0��x��2��0���ֱ����x����1��x��2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx����1��x��2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3���������x����1���ک�1��x��2����x��2��
���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1��0��x��2��0���ֱ����x����1��x��2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx����1��x��2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3���������x����1���ک�1��x��2����x��2��
�Ӷ��������ʽ|x+1|+|x��2|�ɷ�����3�������
�ٵ�x����1ʱ��ԭʽ������x+1������x��2������2x+1��
�ڵ���1��x��2ʱ��ԭʽ��x+1����x��2����3��
�۵�x��2ʱ��ԭʽ��x+1+x��2��2x��1��
�������ۣ�ԭʽ��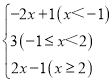
ͨ�������Ķ����������������⣺
��1����x��2ʱ��|x��2|���� ����
��2�����ݲ����еķ����������ʽ|x+2|+|x��4|����д�������̣�
��3��ֱ��д��|x��1|��4|x+1|�����ֵ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬AB=5cm��BC=3cm������P�ӵ�A��������ÿ��2cm���ٶ�������A��C��B��A�˶������˶�ʱ��Ϊt�루t��0����

(1)����P��AC�ϣ�������PA=PBʱ�������ʱt��ֵ��
(2)����Pǡ���ڡ�BAC�Ľ�ƽ�����ϣ���t��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com