
【题目】如图,在菱形 ABCD 中,B 60 ,M 、N 分别为线段 AB 、BC 上的两点,且 BM CN , AN 、CM 相交于点 E 。
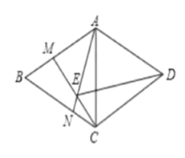
(1)证明: BCM ≌ CAN 。
(2)求AEM 的度数。
(3)证明: AE CE DE 。
【答案】(1)见解析;(2)60°; (3)见解析.
【解析】
(1)由题意可得△ABC,△ADC都是等边三角形,根据SAS即可证明△BCM≌△CAN.
(2)由△BCM≌△CAN,推出∠BCM=∠CAN,推出∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°,作DG⊥AN于G,DH⊥MC交MC的延长线于H,由△DGA≌△DHC,推出DG=DH,由DG⊥AN,DH⊥MC,推出∠DEG=∠DEH,即可得到∠AED的度数.
(3)由(2)可知,∠GED=60°,在Rt△DEG中,由∠EDG =30°,推出DE=2EG,易证△DEG≌△DEH,推出EG=EH,推出EA+EC=EG+AG+EH-CH,由△DGA≌△DHC,推出GA=CH,推出EA+EC=2EG=DE.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
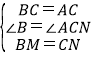 ,
,
∴△BCM≌△CAN(SAS).
(2)∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°,
如图,作DG⊥AN于G,DH⊥MC,交MC的延长线于H,

∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
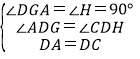 ,
,
∴△DGA≌△DHC(AAS),
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH,
∴DE平分∠AEC,即∠AED=60°.
(3)证明:由(2)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
在△DEG和△DEH中,
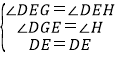 ,
,
∴△DEG≌△DEH(AAS),
∴EG=EH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=EG+AG+EH-CH=2EG=DE.即EA+EC=ED.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某校为了调查学生书写规范汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整)
组别 | 成绩x分 | 频数(人数) |
第1组 | x<60 | 4 |
第2组 | 60≤x<70 | a |
第3组 | 70≤x<80 | 20 |
第4组 | 80≤x<90 | b |
第5组 | 90≤x<100 | 10 |

请结合图表完成下列各题
(1)填空:表中a的值为_______,b的值为_______,扇形统计图中表示第1组所对应的圆心角度数为_______.
(2)若测试成绩不低于80分为优秀,请你估计从该校七年级学生中随机抽查一个学生,他是规范汉字书写优秀的概率是_______;
(3)若测试成绩在60~80分之间(含60分,不含80分)为合格,请你估计则该校七年级学生规范汉字书写不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题中的数据在美国的历史上都是真实的,试对此现象进行分析:
(1) 亚利桑那州历来是一个风景优美,气候宜人的地方,尤其有利于肺结核病人的疗养、康复.可是十九世纪有一位统计学家发现,在亚利桑那州死于肺结核的人数远较其他州多,患者比例普遍达到其他州的 ![]() 至
至 ![]() 倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
(2) 上个世纪,某地的房产开发商曾对当时每户家庭人数进行过较大规模的调查,得到的结论是平均每户 ![]() 人.据此,在当年的住房设计中主要考虑了适宜
人.据此,在当年的住房设计中主要考虑了适宜 ![]() 人家庭居住的户型,结果造成了滞销,而适宜
人家庭居住的户型,结果造成了滞销,而适宜 ![]() 至
至 ![]() 人家庭居住的小户型和
人家庭居住的小户型和 ![]() 人以上的大户型却供不应求.
人以上的大户型却供不应求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 与 BC 相交于 E ,1 2 3, BD CD, ADB 90, CH AB于 H , CH 交 AD 于 F 。
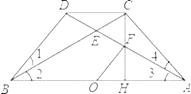
(1)求证: CD∥ AB ;
(2)求证: BDE ≌ ACE ;
(3)若O 为 AB 中点,求证:OF=![]() BE 。
BE 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出a、b、c的值: a=______; b=________; c=________.
(2)a、b、c所对应的点分别为A、B、C,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,试计算此时BC—AB的值.
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和x(x>3)个单位长度的速度向右运动,请问:是否存在x,使BC-AB的值随着时间t的变化而不变,若存在求出x;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④EG![]() BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
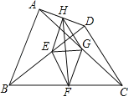
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com