
【题目】以下问题中的数据在美国的历史上都是真实的,试对此现象进行分析:
(1) 亚利桑那州历来是一个风景优美,气候宜人的地方,尤其有利于肺结核病人的疗养、康复.可是十九世纪有一位统计学家发现,在亚利桑那州死于肺结核的人数远较其他州多,患者比例普遍达到其他州的 ![]() 至
至 ![]() 倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
(2) 上个世纪,某地的房产开发商曾对当时每户家庭人数进行过较大规模的调查,得到的结论是平均每户 ![]() 人.据此,在当年的住房设计中主要考虑了适宜
人.据此,在当年的住房设计中主要考虑了适宜 ![]() 人家庭居住的户型,结果造成了滞销,而适宜
人家庭居住的户型,结果造成了滞销,而适宜 ![]() 至
至 ![]() 人家庭居住的小户型和
人家庭居住的小户型和 ![]() 人以上的大户型却供不应求.
人以上的大户型却供不应求.
【答案】(1) 见解析; (2) 见解析.
【解析】试题分析:(1)只关注亚利桑那州死于肺结核的人数远较其他州多,不考虑其他方面,因此是片面的;
(2)平均每户3.6人并不表示大多数家庭规模为近4人,想想应该关注什么数最合适?
试题解析:(1) 由于亚利桑那州的气候、环境有利于肺结核病人的康复,所以必然会有大量外地患者前来疗养,患者比例、死亡人数的增加就不足为奇.要正确评价当地环境对肺结核患者的作用,应同时调查肺结核病人的治愈、好转率,当地居民中肺结核的发病率等.
(2) 平均每户 ![]() 人并不表示大多数家庭规模为近
人并不表示大多数家庭规模为近 ![]() 人.开发商在关注家庭人数平均数、众数的同时应对数据作全面分析,并注重对近期准备购房对象作调查.事实上,当地媒体事后公布的数据是全部家庭中,
人.开发商在关注家庭人数平均数、众数的同时应对数据作全面分析,并注重对近期准备购房对象作调查.事实上,当地媒体事后公布的数据是全部家庭中, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人以上家庭占
人以上家庭占 ![]() ;而两年内购买新房的家庭中
;而两年内购买新房的家庭中 ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人以上家庭占
人以上家庭占 ![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某中学七、八年级各选派10名选手参加知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分选手人数分别为a,b.
(1)请依据图表中的数据,求a,b的值.
(2)直接写出表中的m= ,n= .
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.

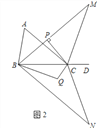
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月23、24日,兰州市九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)这次共抽取了多少名学生的一分钟跳绳测试成绩?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)如果这次测试成绩中的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人?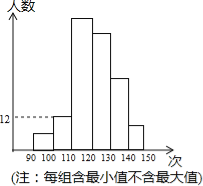
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,B 60 ,M 、N 分别为线段 AB 、BC 上的两点,且 BM CN , AN 、CM 相交于点 E 。
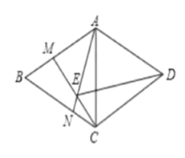
(1)证明: BCM ≌ CAN 。
(2)求AEM 的度数。
(3)证明: AE CE DE 。
查看答案和解析>>
科目:初中数学 来源: 题型:
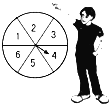
【题目】如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
(1)指针指向4的概率;
(2)指针指向数字是奇数的概率;
(3)指针指向数字不小于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com