
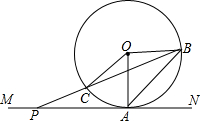
 如图,MN是⊙O的切线,点A为切点,点P是射线AM上的任意一点.点B是⊙O上的一点,连接PB交⊙O于点C.
如图,MN是⊙O的切线,点A为切点,点P是射线AM上的任意一点.点B是⊙O上的一点,连接PB交⊙O于点C.分析 (1)根据三角形的外角等于和它不相邻的两个内角的和,同弧所对的圆心角是圆周角的2倍,可以得到∠AOC的度数;
(2)根据三角形的外角等于和它不相邻的两个内角的和,同弧所对的圆心角是圆周角的2倍,可以用含m、n的代数式表示出∠BOC,本题得以解决.
解答 解:(1)∵∠BAN=45°,∠BPA=30°,∠BAN=∠BPA+∠ABC,
∴∠ABC=15°,
∴∠AOC=2∠ABC=30°,
即∠AOC的度数是30°;
(2)∵∠BAN=n°(n<45),∠BPA=m°,∠BAN=∠BPA+∠ABC,
∴∠ABC=n°-m°,
∴∠AOC=2(n°-m°),
∵∠BAN=n°,∠AOB=2∠BAN,
∴∠AOB=2n°,
∴∠BOC=∠AOB+∠AOC=2n°+2(n°-m°)=4n°-2m°,
即∠BOC与n、m之间的关系是∠BOC=4n°-2m°.
点评 本题考查切线的性质、三角形外角和内角的关系,同弧所对的圆心角和圆心角的关系,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{6}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{8}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,抛物线y=ax2+bx+c经过O、A、E三点.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,抛物线y=ax2+bx+c经过O、A、E三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 33×108元 | B. | 3.3×109元 | C. | 3.3×1010元 | D. | 0.33×1010元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com