
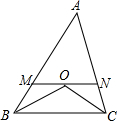
 如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14.
如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14. 科目:初中数学 来源: 题型:解答题
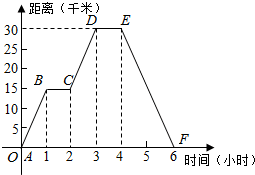 小明同学骑自行车去郊外春游,图中表示的是他离家的距离y(千米)与所用的时间(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,图中表示的是他离家的距离y(千米)与所用的时间(小时)之间关系的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )| A. | $\frac{20}{sin37°}$ | B. | 20tan37° | C. | $\frac{20}{tan37°}$ | D. | 20sin37° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-$\frac{7}{4}$ | B. | k≥-$\frac{7}{4}$ | C. | k≥-$\frac{7}{4}$且k≠0 | D. | k>-$\frac{7}{4}$且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com