
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ![]() ).
). 
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.
【答案】
(1)解:∵反比例函数y= ![]() (k≠0)在第一象限内的图象经过点E(3,
(k≠0)在第一象限内的图象经过点E(3, ![]() ),
),
∴k=3× ![]() =2,
=2,
∴反比例函数的表达式为y= ![]() .
.
又∵点D(m,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴2m=2,解得:m=1
(2)解:设OG=x,则CG=OC﹣OG=2﹣x,
∵点D(1,2),
∴CD=1.
在Rt△CDG中,∠DCG=90°,CG=2﹣x,CD=1,DG=OG=x,
∴CD2+CG2=DG2,即1+(2﹣x)2=x2,
解得:x= ![]() ,
,
∴点G(0, ![]() ).
).
过点F作FH⊥CB于点H,如图所示.
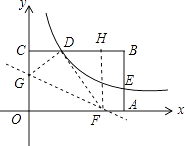
由折叠的特性可知:∠GDF=∠GOF=90°,OG=DG,OF=DF.
∵∠CGD+∠CDG=90°,∠CDG+∠HDF=90°,
∴∠CGD=∠HDF,
∵∠DCG=∠FHD=90°,
∴△GCD∽△DHF,
∴ ![]() =2,
=2,
∴DF=2GD= ![]() ,
,
∴点F的坐标为( ![]() ,0).
,0).
设折痕FG所在直线的函数关系式为y=ax+b,
∴有  ,解得:
,解得:  .
.
∴折痕FG所在直线的函数关系式为y=﹣ ![]() x+
x+ ![]()
【解析】(1)由点E的坐标利用反比例函数图象上点的坐标特征即可求出k值,再由点B在反比例函数图象上,代入即可求出m值;(2)设OG=x,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值,从而得出点G的坐标.再过点F作FH⊥CB于点H,由此可得出△GCD∽△DHF,根据相似三角形的性质即可求出线段DF的长度,从而得出点F的坐标,结合点G、F的坐标利用待定系数法即可求出结论.


科目:初中数学 来源: 题型:
【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币 | 5角硬币 | |
每枚厚度(单位:mm) | 1.8 | 1.7 |
每枚质量(单位:g) | 6.1 | 6.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
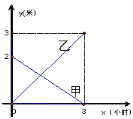
【题目】有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池.甲、乙两个蓄水池中水的深度![]() (米)与注水时间
(米)与注水时间![]() (小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:
(1)注水前甲池中水的深度是_____________米.(直接写出答案).
(2)求甲池中水的深度![]() (米)与注水时间
(米)与注水时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
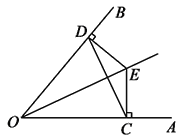
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
(1)求证:ED=EC;
(2)求证:∠ECD=∠EDC;
(3)求证:OE垂直平分CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解.
是方程2x3-x2+m=0的解.
∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0.
+m=0.
∴m=![]() .
.
请你模仿上面的方法尝试解决下面的问题:
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2),求实数m,n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com