
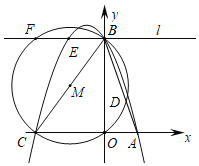
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO![]() ,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为_____.
,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为_____.
【答案】![]() .
.
【解析】
先通过tan∠ABO![]() 及A(1,0)求出点B的坐标,然后将A,B,C代入抛物线的解析式中,求出相应的a,b,e,用含m的式子表示出抛物线的对称轴,利用抛物线的对称性,可得EB,FB的长,进而求出EF的长为定长;连接CD,证明△CAD∽△BAO,列出比例式,将相关线段代入,化简即可求出m的值.
及A(1,0)求出点B的坐标,然后将A,B,C代入抛物线的解析式中,求出相应的a,b,e,用含m的式子表示出抛物线的对称轴,利用抛物线的对称性,可得EB,FB的长,进而求出EF的长为定长;连接CD,证明△CAD∽△BAO,列出比例式,将相关线段代入,化简即可求出m的值.
∵A(1,0),
∴OA=1,
∵tan∠ABO![]() ,
,
∴OB=2,即:点B的坐标为(0,2).
点C(m,0),A(1,0),B(0,2)在抛物线y=ax2+bx+e上,
∴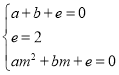 ,
,
解得:b![]() ,a
,a![]() ,
,
∴对称轴x![]() .
.
∵EB=﹣(1+m),FB=﹣m,EF=FB﹣EB=1,
∴线段EF的长是定值1.
∴BD=EF=1.
如图所示,连接CD

∵BC为直径
∴∠CDB=90°
∴∠CDA=∠AOB=90°,∠CAD=∠BAO
∴△CAD∽△BAO
∴![]()
A(1,0),B(0,2),C(m,0),
∴AB![]() ,AC=1﹣m,AO=1
,AC=1﹣m,AO=1
∵BD=1
∴AD![]() 1
1
∴![]()
∴1﹣m=5![]()
∴m![]()
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=![]() (90°﹣∠P)成立.请你写出推理过程.
(90°﹣∠P)成立.请你写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
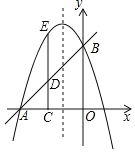
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仿照例题完成任务:
例:如图1,在网格中,小正方形的边长均为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上,
都在格点上,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
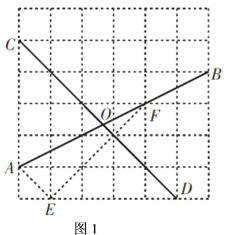
解析:连接![]() ,
,![]() ,导出
,导出![]() ,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
连接![]() ,
,![]() ,则
,则![]() ,
,
![]() ,根据勾股定理可得:
,根据勾股定理可得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]()
即![]() .
.
任务:
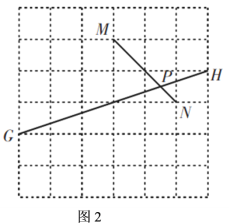
(1)如图2,![]() ,
,![]() ,
,![]() ,
,![]() 四点均在边长为
四点均在边长为![]() 的正方形网格的格点上,线段
的正方形网格的格点上,线段![]() ,
,![]() 相交于点
相交于点![]() ,求图中
,求图中![]() 的正切值;
的正切值;
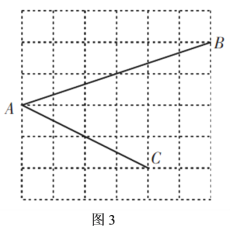
(2)如图3,![]() ,
,![]() ,
,![]() 均在边长为
均在边长为![]() 的正方形网格的格点上,请你直接写出
的正方形网格的格点上,请你直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为![]() .设⊙M与y轴交于D,抛物线的顶点为E.
.设⊙M与y轴交于D,抛物线的顶点为E.
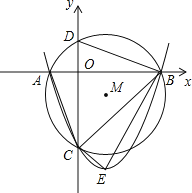
(1)求m的值及抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
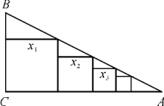
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的n
的n![]() 个正方形依次放入△ABC中,则第n个正方形的边长
个正方形依次放入△ABC中,则第n个正方形的边长![]() _______________(用含n的式子表示).
_______________(用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com