
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为![]() .设⊙M与y轴交于D,抛物线的顶点为E.
.设⊙M与y轴交于D,抛物线的顶点为E.
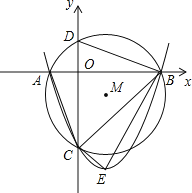
(1)求m的值及抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)m=﹣1,y=x2﹣2x﹣3;(2)sin(α﹣β)=![]() ;(3)在坐标轴上存在三个点P1(0,0),P2(0,
;(3)在坐标轴上存在三个点P1(0,0),P2(0,![]() ),P3(9,0),使得以P、A、C为顶点的三角形与△BCE相似.
),P3(9,0),使得以P、A、C为顶点的三角形与△BCE相似.
【解析】
(1)过M作MN⊥y轴于N,连接CM,利用勾股定理可知m的值,同样的方法可以求出点B的坐标,将点B的坐标代入抛物线解析式中即可求.
(2)通过计算可得出![]() ,进而证明Rt△BOD∽Rt△BCE,得∠CBE=∠OBD=β,则sin(α﹣β)=sin(∠DBC﹣∠OBD)=sin∠OBC可求.
,进而证明Rt△BOD∽Rt△BCE,得∠CBE=∠OBD=β,则sin(α﹣β)=sin(∠DBC﹣∠OBD)=sin∠OBC可求.
(3)经过分析可知,根据题意分Rt△COA∽Rt△BCE;过A作AP2⊥AC交y正半轴于P2,Rt△CAP2∽Rt△BCE;过C作CP3⊥AC交x正半轴于P3,Rt△P3CA∽Rt△BCE三种情况,分情况讨论即可.
(1)由题意可知C(0,﹣3),![]() 1,
1,
∴抛物线的解析式为y=ax2﹣2ax﹣3(a>0),
过M作MN⊥y轴于N,连接CM,
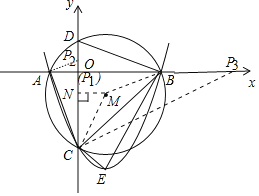
则MN=1,CM![]() ,
,
由勾股定理得CN=2,ON=1,
∴m=﹣1.
同理可求得B(3,0),
将点B代入抛物线的解析式中得
∴a×32﹣2a×3﹣3=0,得a=1.
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)由(1)得A(﹣1,0),E(1,﹣4),B(3,0),C(0,﹣3).
∵M到AB,CD的距离相等,OB=OC,
∴OA=OD,
∴点D的坐标为(0,1),
∴在Rt△BCO中,BC![]() 3
3![]() ,
,
∴![]() ,
,
在△BCE中,
∵BC2+CE2=![]()
![]()
![]()
∴△BCE是Rt△
![]() ,
,
∴![]() ,
,
即![]() ,
,
∴Rt△BOD∽Rt△BCE,得∠CBE=∠OBD=β,
因此sin(α﹣β)=sin(∠DBC﹣∠OBD)=sin∠OBC![]() .
.
(3)∵OB=OC,OD=OA,![]()
![]()
∴Rt△COA∽Rt△BCE,此时点P1(0,0).
过A作AP2⊥AC交y正半轴于P2,
则Rt△CAP2∽Rt△BCE,
![]()
![]()
![]()
![]()
![]()
∴P2(0,![]() ).
).
过C作CP3⊥AC交x正半轴于P3,
则Rt△P3CA∽Rt△BCE,
![]()
![]()
![]()
![]()
![]()
∴P3(9,0).
故在坐标轴上存在三个点P1(0,0),P2(0,![]() ),P3(9,0),
),P3(9,0),
使得以P、A、C为顶点的三角形与△BCE相似.


科目:初中数学 来源: 题型:
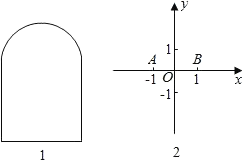
【题目】已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点A(﹣1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,求点C所在的区域的面积;
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
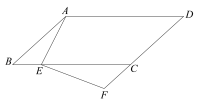
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
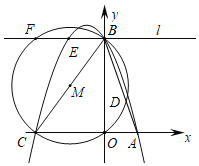
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO![]() ,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为_____.
,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
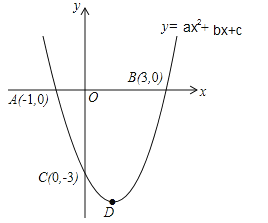
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
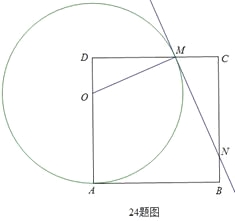
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.

(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com