

分析 根据图形易得:n=1时有1=12个平行四边形;n=2时有2=1×2个平行四边形;n=3时有4=22个平行四边形;n=4时有6=2×3个平行四边形;由此可知应当分n的奇偶,得出答案即可.
解答 解:∵n=1时有1=12个平行四边形;
n=2时有2=1×2个平行四边形;
n=3时有4=22个平行四边形;
n=4时有6=2×3个平行四边形;
…
∴当为第2k-1(k为正整数)个图形时,有k2个平行四边形,
当第2k(k为正整数)个图形时,有k(k+1)个平行四边形,
第2n-1个图形中平行四边形的个数为n2.
故答案为:6,n2.
点评 本题考查了图形的变化规律,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
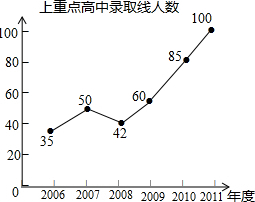 某校近6年来中考上市重点高中录取的情况如图所示:
某校近6年来中考上市重点高中录取的情况如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
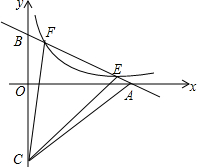 如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.
如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
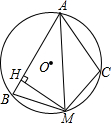 如图,⊙O的内接四边形ABMC中,AB>AC,M是$\widehat{BC}$的中点,MH⊥AB于N,求证:BH=$\frac{1}{2}$(AB-AC).
如图,⊙O的内接四边形ABMC中,AB>AC,M是$\widehat{BC}$的中点,MH⊥AB于N,求证:BH=$\frac{1}{2}$(AB-AC).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com