
分析 (1)先去括号,再移项、合并同类项,不等式两边同乘以$\frac{1}{2}$,即可得出不等式的解集;
(2)先把②整理,再由减法消去x求出y,然后代入①求出x即可,
解答 解:(1)去括号,得:2x-6-2≤0,
移项,得:2x≤6+2,
合并同类项,得:2x≤8,
两边同乘以$\frac{1}{2}$,得:x≤4;
∴原不等式的解集为:x≤4.
(2)由②得:2x-2y=1③,
①-②得:y=4,
把y=4代入①得:x=$\frac{9}{2}$,
∴原方程组的解为:$\left\{\begin{array}{l}x=\frac{9}{2}\\ y=4\end{array}$
点评 本题考查了不等式的解法、二元一次方程组的解法;熟练掌握不等式的解法和用加减法解方程组是解决问题的关键,


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:选择题
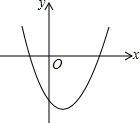 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )| A. | 函数图象与y轴的交点坐标是(0,-3) | |
| B. | 顶点坐标是(1,-3) | |
| C. | 函数图象与x轴的交点坐标是(3,0)、(-1,0) | |
| D. | 当x<0时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
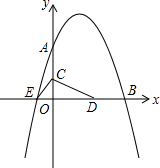 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
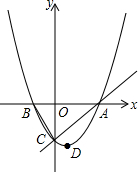 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
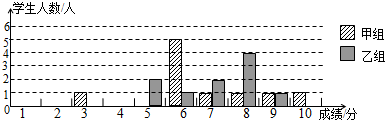
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲 | 6.7 | 6 | 3.41 | 90% | 20% |
| 乙 | 7.1 | 7.5 | 1.69 | 80% | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com