
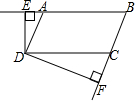
 如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.
如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.  名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
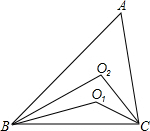 如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB.
如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
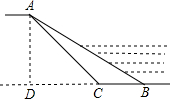 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
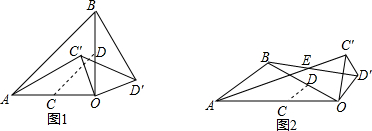
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com