
【题目】等边三角形ABC中,D、E分别是AB、BC上的点,且AD=BE,AE、CD相交于点P,CF⊥AE.
(1)求∠CPE的度数;
(2)求证:PF=![]() PC.
PC.
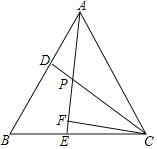
【答案】(1)∠CPE=60°;(2)见详解.
【解析】
(1)先根据已知条件判定出△BEA≌△CAD,得到CD=AE,再结合已知可证△CDB≌△ACE,由此可得∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,即可知∠B=∠CPE=60°;
(2)由CF⊥AE,∠CPE=60°,可得△CPF是含30°角的直角三角形,即可证明.
(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠B,
又∵AD=BE,
∴△BEA≌△CAD,BD=CE,
∴CD=AE,
又∵∠ACB=∠B,
∴△CDB≌△ACE,
∴∠BDC=∠AEC,
∴∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,
∴∠B=∠CPE=60°;
(2)∵CF⊥AE,∠CPE=60°,
∴∠FCP=30°,
∴PF=![]() PC.
PC.


科目:初中数学 来源: 题型:
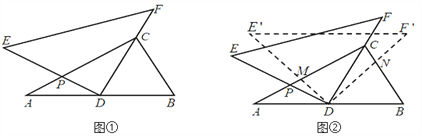
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断![]() 的值是否随着
的值是否随着![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=7cm,CD=5cm,P、Q两点分别从B、C两点同时出发,沿矩形ABCD的边以1cm/s的速度逆时针运动,点P到达点C时两点同时停止运动.当点P的运动时间为_s时,△PQC为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机选取了![]() 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计该校学生同时喜欢短跑和跳绳的概率;
(2)估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
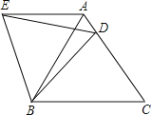
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC; ③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
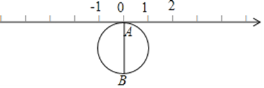
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
查看答案和解析>>
科目:初中数学 来源: 题型:
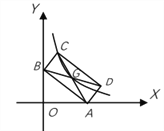
【题目】如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y![]() 经过点C、G,则k=__________.
经过点C、G,则k=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
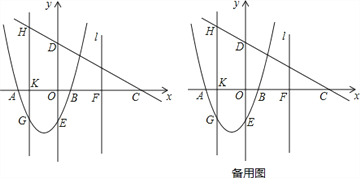
【题目】如图,抛物线y=ax2+bx-3交x轴于点A(﹣3,0),点B(1,0),交y轴于点E.点C是点A关于点B的对称点,点F是线段BC的中点,直线![]() 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线![]() 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com