
【题目】如图,矩形ABCD中,BC=7cm,CD=5cm,P、Q两点分别从B、C两点同时出发,沿矩形ABCD的边以1cm/s的速度逆时针运动,点P到达点C时两点同时停止运动.当点P的运动时间为_s时,△PQC为等腰三角形.

科目:初中数学 来源: 题型:
【题目】如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒3°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)

(1)当t=2时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到63°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而小于180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
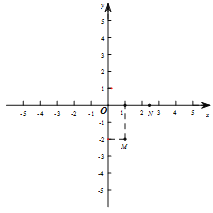
(![]() 为任意实数)经过下图中两点M(1,-2)、N(
为任意实数)经过下图中两点M(1,-2)、N(![]() ,0),其中M为抛物线的顶点,N为定点.下列结论:
,0),其中M为抛物线的顶点,N为定点.下列结论:
①若方程![]() 的两根为
的两根为![]() ,
, ![]() (
(![]() ),则
),则![]() ,
, ![]() ;
;
②当![]() 时,函数值
时,函数值![]() 随自变量
随自变量![]() 的减小而减小.
的减小而减小.
③![]() ,
, ![]() ,
, ![]() .
.
④垂直于![]() 轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为
轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为![]() 、
、![]() ,则
,则![]() =2 .
=2 .
其中正确的是( )
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:如图(1),在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.
(1)写出筝形的两个性质(定义除外).
① ;② .
(2)如图(2),在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(3)如图(3),在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
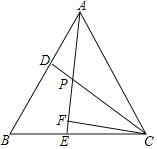
【题目】等边三角形ABC中,D、E分别是AB、BC上的点,且AD=BE,AE、CD相交于点P,CF⊥AE.
(1)求∠CPE的度数;
(2)求证:PF=![]() PC.
PC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
(1)求证:△ACE≌△CBD;
(2)求∠CGE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com