Question

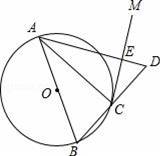
如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线CM．

（1）求证：∠ACM=∠ABC；

（2）延长BC到D，使BC=CD，连接AD与CM交于点E，若⊙O的半径为3，ED=2，求AC的长．

Answer 1

【考点】切线的性质．

【分析】（1）连接OC，由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°，再利用∠BAC=∠ACO，得出结论，

（2）连接OC，得出△AEC是直角三角形，△AEC的外接圆的直径是AC，利用△ABC∽△CDE，求出AC．

【解答】（1）证明：如图，连接OC，

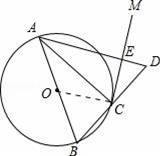
∵AB为⊙O的直径，

∴∠ACB=90°，

∴∠ABC+∠BAC=90°，

又∵CM是⊙O的切线，

∴OC⊥CM，

∴∠ACM+∠ACO=90°，

∵CO=AO，

∴∠BAC=∠ACO，

∴∠ACM=∠ABC；

（2）解：∵BC=CD，∠ACB=90°，

∴∠OAC=∠CAD，

∵OA=OC，

∴∠OAC=∠OCA，

∴∠OCA=∠CAD，

∴OC∥AD，

又∵OC⊥CE，

∴AD⊥CE，

∴△AEC是直角三角形，

∴△AEC的外接圆的直径是AC，

又∵∠ABC+∠BAC=90°，∠ACM+∠ECD=90°，

∴△ABC∽△CDE，

∴=，

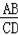
⊙O的半径为3，

∴AB=6，

∴=，

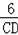
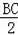
∴BC²=12，

∴BC=2，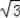

∴AC=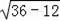=2．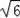

【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了勾股定理、圆周角定理和相似三角形的判定与性质．解题的关键是找准角的关系．