
| 1 |
| 2 |
| 1 |
| 3 |
| 2 | ||
|
| 3 |
|
 解:(1)原式=1+3×
解:(1)原式=1+3×2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
| 1 |
| 3 |
| 1 |
| 3 |


科目:初中数学 来源: 题型:
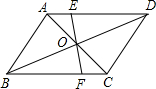 如图,在?ABCD中,对角线AC、BD交于点O,过点O的直线分别交BC、AD于F、E.若AB=4cm,AD=6cm,OE=2cm,则图形EFCD的周长是( )
如图,在?ABCD中,对角线AC、BD交于点O,过点O的直线分别交BC、AD于F、E.若AB=4cm,AD=6cm,OE=2cm,则图形EFCD的周长是( )| A、16cm | B、15cm |
| C、14cm | D、12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
 热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300
热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?
一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?查看答案和解析>>
科目:初中数学 来源: 题型:
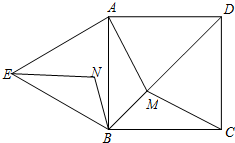 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
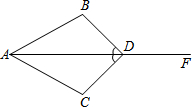 如图所示,∠ADB=∠ADC,
如图所示,∠ADB=∠ADC,查看答案和解析>>
科目:初中数学 来源: 题型:
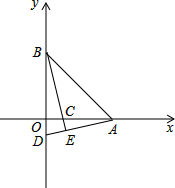 在平面直角坐标系中,已知A,B两点分别在x轴,y轴上,OA=OB=4,C在线段OA上,AC=3,过点A作AE⊥BC,交BC的延长线于E,直线AE交y轴于D.
在平面直角坐标系中,已知A,B两点分别在x轴,y轴上,OA=OB=4,C在线段OA上,AC=3,过点A作AE⊥BC,交BC的延长线于E,直线AE交y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:
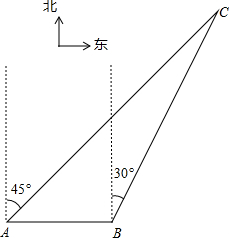 如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场,若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值)
如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场,若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com