
【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E.
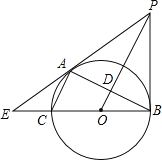
(1)求证:PA是⊙O的切线;(2)若sinE=![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先利用平行线的性质得到∠ACO=∠POB,∠CAO=∠POA,加上∠ACO=∠CAO,则∠POA=∠POB,于是可根据“SAS”判断△PAO≌△PBO,则∠PAO=∠PBO=90°,然后根据切线的判定定理即可得到PA是⊙O的切线;
(2)先由△PAO≌△PBO得PB=PA=6,在Rt△PBE中,利用正弦的定义可计算PE=10,则AE=PE-PA=4,再在Rt△AOE中,由sinE=![]() ,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3
,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3![]() ,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
(1)证明:连接OA,如图,
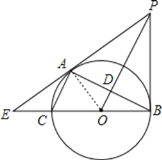
∵AC∥OP,
∴∠ACO=∠POB,∠CAO=∠POA,
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠POA=∠POB,
在△PAO和△PBO中,
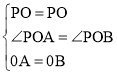 ,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO,
又∵PB⊥BC,
∴∠PBO=90°,
∴∠PAO=90°,
∴OA⊥PE,
∴PA是⊙O的切线;
(2)解:∵△PAO≌△PBO,
∴PB=PA=6,
在Rt△PBE中,∵sinE=![]()
∴![]() ,解得PE=10,
,解得PE=10,
∴AE=PE﹣PA=4,
在Rt△AOE中,sinE=![]() ,
,
设OA=3t,则OE=5t,
∴AE=![]() =4t,
=4t,
∴4t=4,解得t=1,
∴OA=3,
在Rt△PBO中,∵OB=3,PB=6,
∴OP=![]() ,
,
∵AC∥OP,
∴△EAC∽△EPO,
∴![]() ,即
,即![]() ,
,
∴AC=![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
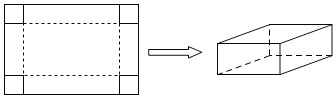
【题目】如图,工人师傅用一块长为10分米,宽为6分米的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形;(厚度不计)
(1)当长方体底面面积为12平方分米时,裁掉的正方形边长为______分米;
(2)若要求制作的长方体的底面长不大于底面宽的5倍,且将容器的外表面进行防锈处理,其侧面处理费用为0.5元/平方分米,底面处理费用为2元/平方分米;求:裁掉的正方形边长为多大时,防锈处理总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学的课余生活,某学校将举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是________”的问卷调查,要求学生只能从“A(绿博园),B(人民公园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
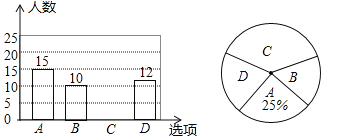
回答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校共有3 600名学生,试估计该校去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市为了缓解停车难的问题,建筑设计师提供了楼顶停车场的设计示意图(如图AC与ME平行).按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.请根据下图求出汽车通过坡道口的限高DF的长.(结果精确到0.1m)
(参考数据: sin28°≈0.47,cos28°≈0.88, tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .
.
(1)如图1,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,当
,当![]() ,
,![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)如图2,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
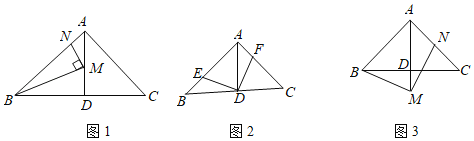
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).

(1)将△ABC沿![]() 轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点O顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2 、C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com