
【题目】如图Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A出发沿AB边以1cm/秒的速度向点B匀速移动,同时,点Q从点B出发沿BC边以2cm/秒的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动( )秒后,△PBQ面积为5cm2.
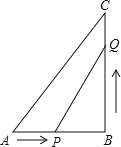
A.0.5B.1C.5D.1或5
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】对于给定函数y=a1x2+b1x+c1(其中a1、b1、c1为常数,且a1≠0),则称函数y= (a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(1)已知函数y=﹣x2+4x+2.
①直接写出这个函数的“相关函数”;
②若点P(a,1)在“相关函数”的图象上,求a的值;
③若直线y=m与图象G恰好有两个公共点,直接写出m的取值范围;
(2)设函数y=﹣![]() x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当
x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出n的取值范围.
≤y0≤9时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
“美化城市,改善人民居住环境”是城市建设的一项重要内容.某市近年来,通过植草、栽树、修建公园等措施,使城区绿地面积不断增加,2011年底该市城区绿地总面积约为75公顷,截止到2013年底,该市城区绿地总面积约为108公顷,求从2011年底至2013年底该市城区绿地总面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com