
【题目】国家支持大学生创新办实业,提供小额无息贷款.学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额﹣成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
【答案】
(1)解:设y=kx+b(k≠0),
由题意得: ![]() ,
,
解得 ![]() ,
,
∴y=﹣2x+140
(2)解:当x=48时,y=﹣2x+140=44.
设该店员工有a人,
则(48﹣40)×44=82a+106,
解得a=3.
答:该店员工有3人
(3)解:设每天的利润为W(元),由题意,得
W=(x﹣40)y=(x﹣40)(﹣2x+140)
=﹣2(x﹣55)2+450.
设至少需要b天能还清所有贷款由题意,得
450b≥(82×2+106)b+36000.
解得b≥200.
答:该店至少需要200天能还清所有贷款,此时每件服装的价格应定为55元
【解析】(1)利用待定系数法求解可得;(2)由售价依据(1)中函数解析式求得销售量,继而根据“(售价﹣进价)×销售量=员工人数×每人每天工资+其他开支”列方程求解可得;(3)先依据:总利润=单件利润×销售量列出函数解析式,求得每天毛利润的最大值,继而根据利润最大值×天数≥每天的总支出×天数+贷款钱数,解不等式可得答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
A.-4
B.4
C.-2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M(4,0),以点M为圆心,2为半径的圆与x轴交于点A、B,已知抛物线y= ![]() x2+bx+c过点A和B,与y轴交于点C.
x2+bx+c过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点P为此抛物线对称轴上一个动点,求PC﹣PA的最大值.
(3)CE是过点C的⊙M的切线,E是切点,CE交OA于点D,求OE所在直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且 ![]() =
= ![]() ,弦AD的延长线交切线PC于点E,连接AC.
,弦AD的延长线交切线PC于点E,连接AC. 
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP= ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,﹣3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.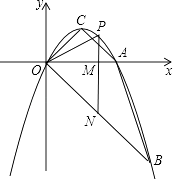
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为;当△PMO∽△COB时,点P的坐标为;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com