
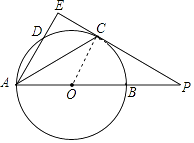
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且 ![]() =
= ![]() ,弦AD的延长线交切线PC于点E,连接AC.
,弦AD的延长线交切线PC于点E,连接AC. 
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP= ![]() ,求AE的长.
,求AE的长.
【答案】
(1)解:连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵BC=CD,
∴∠OAC=∠CAD.
∴∠OCA=∠CAD,
∴OC∥AE.
∴∠E=∠OCP.
∵PE是的切线,C为切点,
∴∠OCP=90°.
∴∠E=90°
(2)解:在Rt△ABD中,OC=2.5,sin∠P= ![]() =
= ![]() ,
,
∴OP= ![]() ,
,
在Rt△APE中,AP= ![]() +2.5=
+2.5= ![]() ,sin∠P=
,sin∠P= ![]() =
= ![]() ,
,
∴AE=4.
【解析】(1)连接OC.根据等腰三角形的性质得到∠OAC=∠OCA.∠OAC=∠CAD.推出OC∥AE.根据平行线的性质得到∠E=∠OCP.根据切线的性质即可得到结论;(2)解直角三角形即可得到结论.
【考点精析】利用切线的性质定理和解直角三角形对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
A.AF=AE
B.△ABE≌△AGF
C.EF=![]()
D.AF=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌子上放着背面完全相同的4张扑克牌,其中有一张大王,小明和小红玩“抽大王”游戏,两人各抽取一次(每次都不放回),抽到大王者获胜,小明先抽,小红后抽,求小红获胜的概率.(请用“画树状图”或“列表”等方法,写出分析过程,并给出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款.学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额﹣成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D在边AB上,连接CD,将△BCD沿CD翻折得到△ECD,使DE∥AC,CE交AB于点F,若∠B=α,则∠ADC的度数是 (用含α的代数式表示).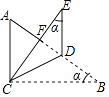
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G.
(1)求证:FG=BG;
(2)若AB=6,BC=4,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=﹣ ![]() x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大?若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠A=30°,BC=4.若DE是△ABC的中位线,延长DE交∠ACM的平分线于点F,则DF的长为( ) 
A.6
B.7
C.8
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com