
【题目】已知:如图,直线y=﹣ ![]() x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大?若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.
【答案】
(1)
解:(1)在y=﹣ ![]() x﹣3中,当y=0时,x=﹣6,
x﹣3中,当y=0时,x=﹣6,
即点A的坐标为:(﹣6,0),
将A(﹣6,0),B(2,0)代入y=ax2+bx﹣3得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y= ![]() x2+x﹣3;
x2+x﹣3;
(2)
解:设点D的坐标为:(m, ![]() m2+m﹣3),则点F的坐标为:(m,﹣
m2+m﹣3),则点F的坐标为:(m,﹣ ![]() m﹣3),
m﹣3),
∴DF=﹣ ![]() m﹣3﹣(
m﹣3﹣( ![]() m2+m﹣3)=﹣
m2+m﹣3)=﹣ ![]() m2﹣
m2﹣ ![]() m,
m,
∴S△ADC=S△ADF+S△DFC
= ![]() DFAE+
DFAE+ ![]() DFOE
DFOE
= ![]() DFOA
DFOA
= ![]() ×(﹣
×(﹣ ![]() m2﹣
m2﹣ ![]() m)×6
m)×6
=﹣ ![]() m2﹣
m2﹣ ![]() m
m
=﹣ ![]() (m﹣3)2+
(m﹣3)2+ ![]() ,
,
∵a=﹣ ![]() <0,
<0,
∴抛物线开口向下,
∴当m=3时,S△ADC存在最大值 ![]() ,
,
又∵当m=3时, ![]() m2+m﹣3=﹣
m2+m﹣3=﹣ ![]() ,
,
∴存在点D(3,﹣ ![]() ),使得△ADC的面积最大,最大值为
),使得△ADC的面积最大,最大值为 ![]() ;
;
(3)
解:由题意可得△ADE的面积分成1:4两部分即是点F将DE分成1:4两部分
①当DF:EF=1:4时,(﹣ ![]() m2﹣
m2﹣ ![]() m):(
m):( ![]() m+3)=1:4,
m+3)=1:4,
解得:m1=﹣ ![]() ,m2=﹣6(不合题意,舍去),
,m2=﹣6(不合题意,舍去),
当m=﹣ ![]() 时,
时, ![]() m2+m﹣3=﹣
m2+m﹣3=﹣ ![]() ,
,
∴点D的坐标为:(﹣ ![]() ,﹣
,﹣ ![]() ),
),
②当DF:EF=4:1时,(﹣ ![]() m2﹣
m2﹣ ![]() m):(
m):( ![]() m+3)=4:1,
m+3)=4:1,
解得:m1=﹣6(不合题意,舍去),m2=﹣8(不合题意,舍去),
综上所述存在点D(﹣ ![]() ,﹣
,﹣ ![]() ),使得AC恰好将△ADE的面积分成1:4两部分.
),使得AC恰好将△ADE的面积分成1:4两部分.
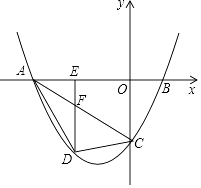
【解析】解:(1)在y=﹣ ![]() x﹣3中,当y=0时,x=﹣6,即点A的坐标为:(﹣6,0),将A(﹣6,0),B(2,0)代入y=ax2+bx﹣3得:
x﹣3中,当y=0时,x=﹣6,即点A的坐标为:(﹣6,0),将A(﹣6,0),B(2,0)代入y=ax2+bx﹣3得: ![]() ,
,
解得: ![]() ,∴抛物线的解析式为:y=
,∴抛物线的解析式为:y= ![]() x2+x﹣3;(2)设点D的坐标为:(m,
x2+x﹣3;(2)设点D的坐标为:(m, ![]() m2+m﹣3),则点F的坐标为:(m,﹣
m2+m﹣3),则点F的坐标为:(m,﹣ ![]() m﹣3),∴DF=﹣
m﹣3),∴DF=﹣ ![]() m﹣3﹣(
m﹣3﹣( ![]() m2+m﹣3)=﹣
m2+m﹣3)=﹣ ![]() m2﹣
m2﹣ ![]() m,∴S△ADC=S△ADF+S△DFC=
m,∴S△ADC=S△ADF+S△DFC= ![]() DFAE+
DFAE+ ![]() DFOE=
DFOE= ![]() DFOA=
DFOA= ![]() ×(﹣
×(﹣ ![]() m2﹣
m2﹣ ![]() m)×6=﹣
m)×6=﹣ ![]() m2﹣
m2﹣ ![]() m=﹣
m=﹣ ![]() (m﹣3)2+
(m﹣3)2+ ![]() ,∵a=﹣
,∵a=﹣ ![]() <0,∴抛物线开口向下,∴当m=3时,S△ADC存在最大值
<0,∴抛物线开口向下,∴当m=3时,S△ADC存在最大值 ![]() ,又∵当m=3时,
,又∵当m=3时, ![]() m2+m﹣3=﹣
m2+m﹣3=﹣ ![]() ,∴存在点D(3,﹣
,∴存在点D(3,﹣ ![]() ),使得△ADC的面积最大,最大值为
),使得△ADC的面积最大,最大值为 ![]() ;(3)由题意可得△ADE的面积分成1:4两部分即是点F将DE分成1:4两部分①当DF:EF=1:4时,(﹣
;(3)由题意可得△ADE的面积分成1:4两部分即是点F将DE分成1:4两部分①当DF:EF=1:4时,(﹣ ![]() m2﹣
m2﹣ ![]() m):(
m):( ![]() m+3)=1:4,解得:m1=﹣
m+3)=1:4,解得:m1=﹣ ![]() ,m2=﹣6(不合题意,舍去),当m=﹣
,m2=﹣6(不合题意,舍去),当m=﹣ ![]() 时,
时, ![]() m2+m﹣3=﹣
m2+m﹣3=﹣ ![]() ,∴点D的坐标为:(﹣
,∴点D的坐标为:(﹣ ![]() ,﹣
,﹣ ![]() ),②当DF:EF=4:1时,(﹣
),②当DF:EF=4:1时,(﹣ ![]() m2﹣
m2﹣ ![]() m):(
m):( ![]() m+3)=4:1,解得:m1=﹣6(不合题意,舍去),m2=﹣8(不合题意,舍去),综上所述存在点D(﹣
m+3)=4:1,解得:m1=﹣6(不合题意,舍去),m2=﹣8(不合题意,舍去),综上所述存在点D(﹣ ![]() ,﹣
,﹣ ![]() ),使得AC恰好将△ADE的面积分成1:4两部分.
),使得AC恰好将△ADE的面积分成1:4两部分.
【考点精析】利用二次函数的最值对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且 ![]() =
= ![]() ,弦AD的延长线交切线PC于点E,连接AC.
,弦AD的延长线交切线PC于点E,连接AC. 
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP= ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD. 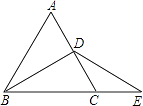
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);
(2)若AB=2,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,﹣3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.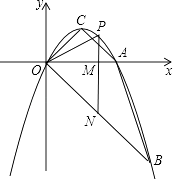
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为;当△PMO∽△COB时,点P的坐标为;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= ![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题: ①存在函数y=
的一个“派生函数”.现给出以下两个命题: ①存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
②函数y= ![]() 的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
A.命题①与命题②都是真命题
B.命题①与命题②都是假命题
C.命题①是假命题,命题②是真命题
D.命题①是真命题,命题②是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com