
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,﹣3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.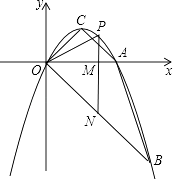
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为;当△PMO∽△COB时,点P的坐标为;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
【答案】
(1)
解:根据题意,得 ![]() ,解这个方程组得
,解这个方程组得 ![]()
∴抛物线的解析式为y=﹣x2+2x
当x=﹣ ![]() =1时,y=﹣x2+2x=1,
=1时,y=﹣x2+2x=1,
∴C(1,1)
(2)(1,﹣1),(2,﹣2),(3﹣ ![]() ,
, ![]() ﹣3);(
﹣3);( ![]() ,
, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() )
)
(3)
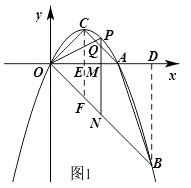
如图1,作BD⊥x轴于D,作CE⊥x轴于E,交OB于F
则BD=OD=3,CE=OE=1,OC=AC
∴△ODB,△OCE,△AOC均为等腰直角三角形,
∴S四边形ABOC=S△OAC+S△OAB= ![]() +
+ ![]() OABD=4
OABD=4
∴∠AOC=∠AOB=∠OAC=45°
∵PM∥y轴,
∴OM⊥PN,∠MNO=∠AOB=45°,
∴OM=MN=m,OE=EF=1
①∵S△OCF= ![]() CFOE=1
CFOE=1 ![]() ×4
×4
∴当0<m≤1时,不能满足条件,
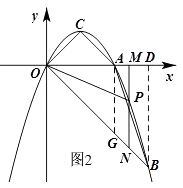
②当1<m≤2时,如图2,设PN交AC于Q,则MQ=MA=2﹣m,
S四边形OCQN=S△OAC+S△OMN﹣S△AMQ= ![]() OACE+
OACE+ ![]() OMMN﹣
OMMN﹣ ![]() AMMQ=2m﹣1,
AMMQ=2m﹣1,
由S四边形OCQM= ![]() S四边形ABOC,得2m﹣1=
S四边形ABOC,得2m﹣1= ![]() ×4,解得m=
×4,解得m= ![]() ,
,
而1< ![]() <2,符合题意,
<2,符合题意,
由S四边形OCQN= ![]() S四边形ABOC,得2m﹣1=
S四边形ABOC,得2m﹣1= ![]() ,解得m=
,解得m= ![]()
而1< ![]() <2,符合题意,
<2,符合题意,
③当2<m<3时,如图2,作AG⊥x轴,交OB于G,
则AG=OA=2,AD=1
∴S△ABG= ![]() AGAD=1<
AGAD=1< ![]() ×4
×4
∴当2<m<3时,不能满足条件
∴m= ![]() 或m=
或m= ![]() .
.
【解析】(2)①∵B(3,﹣3),
∴直线OB的解析式为y=﹣x,
∵P的横坐标为m(0<m<3),
∴P(m,﹣m2+2m),
∴N(m,﹣m),
∴PN2=(﹣m2+3m)2 , OP2=m2+(﹣m2+2m)2 , ON2=2m2 ,
当△PON为等腰三角形时,
①当OP=ON时,m2+(﹣m2+2m)2=2m2 ,
∴m=0(舍)或m=1或m=3(舍),
∴N(1,﹣1)
②当OP=PN时,(﹣m2+3m)2=m2+(﹣m2+2m)2 ,
∴m=0(舍)或m=2,
∴N(2,﹣2),
③当ON=PN时,(﹣m2+3m)2=2m2 ,
∴m=0(舍)或m=3+ ![]() (舍)或m=3﹣
(舍)或m=3﹣ ![]() ,
,
∴N(3﹣ ![]() ,
, ![]() ﹣3),
﹣3),
所以答案是:(1,﹣1),(2,﹣2),(3﹣ ![]() ,
, ![]() ﹣3)
﹣3)
②∵P的横坐标为m(0<m<3),
∴P(m,﹣m2+2m),
∴M(m,0),
∴PM=|﹣m2+2m|,OM=m,
∵B(3,﹣3),
∴OB=3,
由(1)知,C(1,1),
∴OC=1,
∵△PMO∽△COB,
∴ ![]() ,
,
∴ ![]() ,
,
∴m= ![]() 或m=
或m= ![]() ,
,
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() ),
),
所以答案是:( ![]() ,
, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),
),
【考点精析】利用等腰直角三角形和等腰三角形的性质对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款.学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额﹣成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=﹣ ![]() x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
x﹣3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大?若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,tanA= ![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的 ![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的 ![]() 时,已抢修道路米;
时,已抢修道路米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 , 旋转角是度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠A=30°,BC=4.若DE是△ABC的中位线,延长DE交∠ACM的平分线于点F,则DF的长为( ) 
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示) 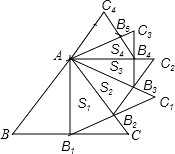
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com