
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示) 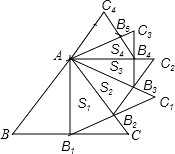
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,﹣3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.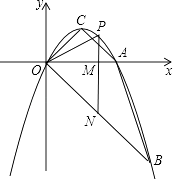
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为;当△PMO∽△COB时,点P的坐标为;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= ![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题: ①存在函数y=
的一个“派生函数”.现给出以下两个命题: ①存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
②函数y= ![]() 的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
A.命题①与命题②都是真命题
B.命题①与命题②都是假命题
C.命题①是假命题,命题②是真命题
D.命题①是真命题,命题②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( ) 
A.105°
B.110°
C.130°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数数值如下: sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
(1)求sin135°,cos150°的值;
(2)若一个三角形的三个内角的比为1:1:4,A,B是这个三角形的两个顶点,且∠A≤∠B,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m值及∠A,∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图. 
(1)请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
A.①②
B.①④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF 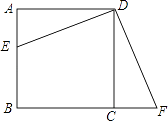
(1)求证:△AED≌△CFD;
(2)将△AED按逆时针方向至少旋转多少度才能与△CFD重合,旋转中心是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m,n的夹角为35°,相交于点O,
(1)作出△ABC关于直线m的对称△DEF;
(2)作出△DEF关于直线n的对称△PQR;
(3)△PQR还可以由△ABC经过一次怎样的变换得到.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com