
【题目】如图,点M(4,0),以点M为圆心,2为半径的圆与x轴交于点A、B,已知抛物线y= ![]() x2+bx+c过点A和B,与y轴交于点C.
x2+bx+c过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点P为此抛物线对称轴上一个动点,求PC﹣PA的最大值.
(3)CE是过点C的⊙M的切线,E是切点,CE交OA于点D,求OE所在直线的函数关系式.
【答案】
(1)
解:由题意,得
A(2,0),B(6,0).
将A,B点坐标代入函数解析式,得
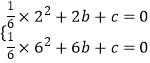 ,
,
解得 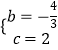 ,
,
函数解析式为y═ ![]() x2﹣
x2﹣ ![]() x+2,
x+2,
当x=0时,y=2,即C点坐标为(0,2),
图象如图1
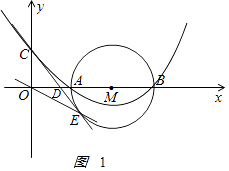
(2)
解:由三角形的两边之差小于第三边,得
PC﹣PA<CA,
当时P,A,C在同一条直线上时,PC﹣PA=AC ![]() =2
=2 ![]() ,
,
即PC﹣PA的最大值是2 ![]()
(3)
解:如图2
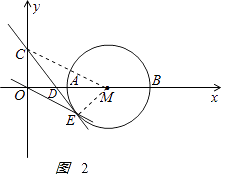 ,
,
连接MC,ME,
∵CE是过点C的⊙M的切线,E是切点,
∴∠MED=∠COD=90°.
在△CDO和△MED中,
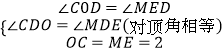 ,
,
∴△CDO≌△MED(AAS),
DO=DE,DC=DM,
∠DEO=∠DOE,∠MCD=∠CMD.
∵∠DEO= ![]() ,∠MCD=
,∠MCD= ![]() ,
,
∴∠MCE=∠CEO,
∴CM∥OE,
∵直线CM的解析式为y=﹣ ![]() x+2,
x+2,
∴直线OE的解析式为y=﹣ ![]() x
x
【解析】(1)根据待定系数法,可得函数解析式,根据自变量与函数值得对应关系,可得C点坐标;(2)根据三角形三边的关系,可得PC﹣PA<CA,根据线段的和差,可得答案;(3)根据全等三角形的判定与性质,可得DO=DE,DC=DM,根据等腰三角形的性质,三角形的内角和,可得∠MCE=∠CEO,根据平行线的判定与性质,可得答案.
【考点精析】本题主要考查了平行线的判定与性质和三角形三边关系的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,E是CD上的一点,连接BE交AC于O,连接DO并延长交BC于E.
(1)求证:△FOC≌△EOC;
(2)将此图中的AD、BE分别延长交于点N,作EM∥BC交CN于M,再连接FM即得到图2.
求证:①![]() ;②FD=FM.
;②FD=FM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为人,m= , n=;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的伴随直线为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的伴随直线为y=2(x+1)﹣3,即y=2x﹣1.
(1)在上面规定下,抛物线y=(x+1)2﹣4的顶点坐标为 , 伴随直线为 , 抛物线y=(x+1)2﹣4与其伴随直线的交点坐标为和;
(2)如图,顶点在第一象限的抛物线y=m(x﹣1)2﹣4m与其伴随直线相交于点A,B(点A在点B的右侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值 ![]() 时,求m的值.
时,求m的值.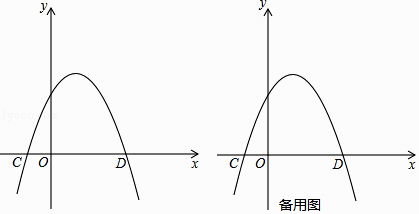
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌子上放着背面完全相同的4张扑克牌,其中有一张大王,小明和小红玩“抽大王”游戏,两人各抽取一次(每次都不放回),抽到大王者获胜,小明先抽,小红后抽,求小红获胜的概率.(请用“画树状图”或“列表”等方法,写出分析过程,并给出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是cm. 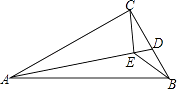
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款.学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额﹣成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D在边AB上,连接CD,将△BCD沿CD翻折得到△ECD,使DE∥AC,CE交AB于点F,若∠B=α,则∠ADC的度数是 (用含α的代数式表示).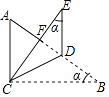
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,tanA= ![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com