
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
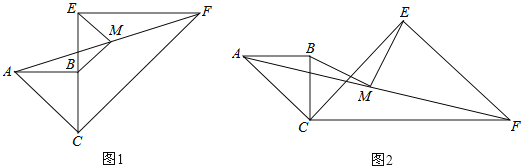
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
【答案】(1)证明见解析;(2)BM=ME=![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)如图1,延长AB交CF于点D,证明BM为△ADF的中位线即可.
(2)如图2,作辅助线,推出BM、ME是两条中位线.
(3)如图3,作辅助线,推出BM、ME是两条中位线:BM=![]() DF,ME=
DF,ME=![]() AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
(1)如图1,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,
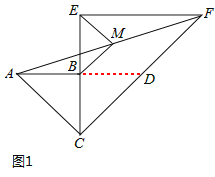
∴AB=BC=BD.
∴点B为线段AD的中点.
又∵点M为线段AF的中点,
∴BM为△ADF的中位线.
∴BM∥CF.
(2)如图2,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,
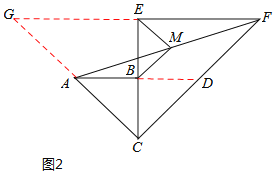
∴AB=BC=BD=a,AC=AD=![]() a,
a,
∴点B为AD中点,又点M为AF中点.
∴BM=![]() DF.
DF.
分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=![]() a.
a.
∴点E为FG中点,又点M为AF中点.
∴ME=![]() AG.
AG.
∵CG=CF=![]() a,CA=CD=
a,CA=CD=![]() a,∴AG=DF=
a,∴AG=DF=![]() a.
a.
∴BM=ME=![]() .
.
(3)如图3,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,
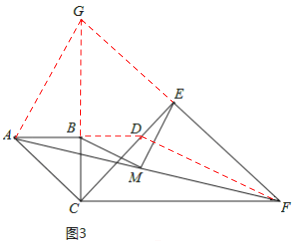
∴AB=BC=BD,AC=CD.
∴点B为AD中点.
又点M为AF中点,∴BM=![]() DF.
DF.
延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=EG,CF=CG.
∴点E为FG中点.
又点M为AF中点,∴ME=![]() AG.
AG.
在△ACG与△DCF中,∵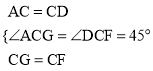 ,
,
∴△ACG≌△DCF(SAS).
∴DF=AG,∴BM=ME.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】红星中学九年级(1)班三位教师决定带领本班![]() 名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
(1)用含![]() 的式子表示三位教师和
的式子表示三位教师和![]() 位学生参加这两家旅行社所需的费用各是多少元;
位学生参加这两家旅行社所需的费用各是多少元;
(2)如果![]() =50时,请你计算选择哪一家旅行社较为合算?
=50时,请你计算选择哪一家旅行社较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
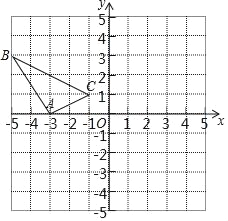
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
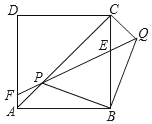
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
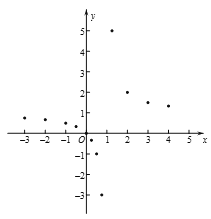
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是 ;
(2)下表是y与x的几组对应数值:

①写出m的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;
(3)当![]() 时,直接写出x的取值范围为 .
时,直接写出x的取值范围为 .
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出![]() 关于直线x=-1对称的
关于直线x=-1对称的![]() ,并写出
,并写出![]() 各点坐标.
各点坐标.
(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
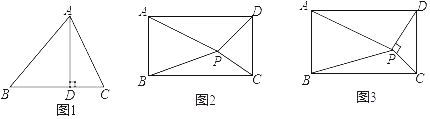
【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
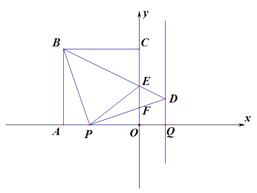
【题目】如图,边长为![]() 正方形OABC的边OA、OC在坐标轴上.在
正方形OABC的边OA、OC在坐标轴上.在![]() 轴上线段
轴上线段![]() (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为
(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为![]() .连接PB,过P作PB的垂线,过Q作
.连接PB,过P作PB的垂线,过Q作![]() 轴的垂线,两垂线相交于点D.连接BD交
轴的垂线,两垂线相交于点D.连接BD交![]() 轴于点E,连接PD交
轴于点E,连接PD交![]() 轴于点F,连接PE.
轴于点F,连接PE.
(1)求∠PBD的度数.
(2)设△POE的周长为![]() ,探索
,探索![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
(3)令![]() ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com