
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΈΣ![]() ’ΐΖΫ–ΈOABCΒΡ±ΏOAΓΔOC‘ΎΉχ±ξ÷α…œ.‘Ύ
’ΐΖΫ–ΈOABCΒΡ±ΏOAΓΔOC‘ΎΉχ±ξ÷α…œ.‘Ύ![]() ÷α…œœΏΕΈ
÷α…œœΏΕΈ![]() Θ®Q‘ΎAΒΡ”“±ΏΘ©Θ§P¥”A≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»œρO‘ΥΕ·Θ§Β±ΒψPΒΫ¥οΒψO ±ΆΘ÷Ι‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣ
Θ®Q‘ΎAΒΡ”“±ΏΘ©Θ§P¥”A≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»œρO‘ΥΕ·Θ§Β±ΒψPΒΫ¥οΒψO ±ΆΘ÷Ι‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣ![]() .Ν§Ϋ”PBΘ§ΙΐPΉςPBΒΡ¥ΙœΏΘ§ΙΐQΉς
.Ν§Ϋ”PBΘ§ΙΐPΉςPBΒΡ¥ΙœΏΘ§ΙΐQΉς![]() ÷αΒΡ¥ΙœΏΘ§ΝΫ¥ΙœΏœύΫΜ”ΎΒψD.Ν§Ϋ”BDΫΜ
÷αΒΡ¥ΙœΏΘ§ΝΫ¥ΙœΏœύΫΜ”ΎΒψD.Ν§Ϋ”BDΫΜ![]() ÷α”ΎΒψEΘ§Ν§Ϋ”PDΫΜ
÷α”ΎΒψEΘ§Ν§Ϋ”PDΫΜ![]() ÷α”ΎΒψFΘ§Ν§Ϋ”PE.
÷α”ΎΒψFΘ§Ν§Ϋ”PE.
Θ®1Θ©«σΓœPBDΒΡΕ» ΐ.
Θ®2Θ©…ηΓςPOEΒΡ÷ή≥ΛΈΣ![]() Θ§ΧΫΥς
Θ§ΧΫΥς![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ω
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
Θ®3Θ©Νν![]() Θ§Β±ΓςPBEΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σΓςEFDΒΡΟφΜΐ.
Θ§Β±ΓςPBEΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σΓςEFDΒΡΟφΜΐ.
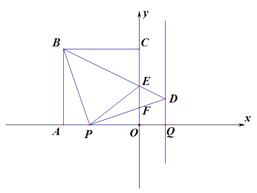
ΓΨ¥πΑΗΓΩ(1)ΓœPBD=45Γψ (2) ![]() ΓΓΓΓ(3)
ΓΓΓΓ(3) ![]() Μρ
Μρ![]() ΓΘ
ΓΘ
ΓΨΫβΈωΓΩΘ®1Θ©“Ή÷ΛBAPΓ’PQDΘ§¥”ΕχΒΟΒΫDQ=AP=tΘ§¥”ΕχΩ…“‘«σ≥ωΓœPADΒΡΕ» ΐ.
Θ®2Θ©”…”ΎΓœEBP=45ΓψΘ§Ι ΆΦ1 «“‘’ΐΖΫ–ΈΈΣ±≥ΨΑΒΡ“ΜΗωΜυ±ΨΆΦ–ΈΘ§Ϋη÷ζ”Ύ»ΐΫ«–Έ»ΪΒ»”…l=EP+PO+EO=(CE+EO)+(AP+PO)=2AOΫχ––«σΫβΘ§»ΜΚσΫαΚœΧθΦΰΫχ––»Γ…αΘ§Ήν÷’»ΖΕ®tΒΡ»Γ÷ΒΖΕΈß÷ΒΘΜΘ®3Θ©œ»÷ΛΟς»ΐΫ«–Έ»ΪΒ»Θ§‘Ό«σ≥ωEFΘ§Φ¥Ω…ΒΟ≥ωΟφΜΐΘ°
ΫβΘΚ(1) ΓΏΓœAPB+ΓœPBA=ΓœAPB+ΓœDPQ=90Γψ
ΓύΓœPBA=ΓœDPQ
”÷ΓΏΓœBAP=ΓœPQD=90Γψ,BA=PQ=![]()
ΓύΓςBAPΓ’ΓςPQD
ΓύBP=PD
”÷ΓΏBPΓΆPD
ΓύΓœPBD=45Γψ
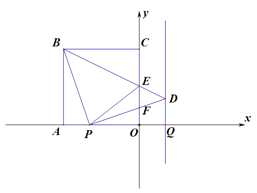
(2)―”≥ΛPA÷ΝMΘ§ ΙΒΟAM=CE
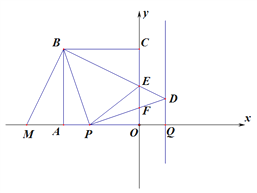
‘ΎΓςBAM”κΓςBCE÷–
ΓΏ
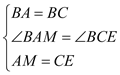
ΓύΓςBAMΓ’ΓςBCE
ΓύΓœMBA=ΓœEBC
ΓΏΓœEBC+ΓœABP=45Γψ
ΓύΓœMBP=ΓœMBA+ΓœABP=45Γψ=ΓœEBP
‘ΎΓςBPM”κΓςBPE÷–
ΓΏ
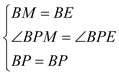
ΓύΓςBPMΓ’ΓςBPE
ΓύEP=MP=MA+AP=CE+AP
”÷ΓΏl=EP+PO+EO=(CE+EO)+(AP+PO)=2AO
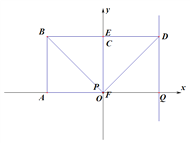
Γύ![]() ΓΓΓΓ
ΓΓΓΓ
(3)EP=EB
ΓΏΓœPBD=45Γψ
ΓύEPΓΆEB Θ§EΈΣBD÷–ΒψΘ§
Φ¥E”κC÷ΊΚœΘ§P”κO÷ΊΚœ
¥Υ ±Θ§SΓςEFD=8Θ§ΓΓ
PB=PE
ΓΏΓœPBD=45Γψ
ΓύEPΓΆPB (≤Μ¥φ‘Ύ)
BP=BE
ΓΏBA=BC
ΓύΓςBAPΓ’ΓςBCE ΓύCE=AP=t![]() ΓύPE=2t
ΓύPE=2t
”÷ΓΏOE=OP=![]() ΓύPE=
ΓύPE=![]() Γύ
Γύ![]() =
=![]() ΫβΒΟΘΚ
ΫβΒΟΘΚ![]()
ΓΏΓςBAPΓ’ΓςPQD ΓύAP=QD ΓύD![]()
ΓΏP![]() Γύ
Γύ![]()
![]() ΓύF
ΓύF![]()
ΓύEF=![]()
¥Υ ±Θ§![]() ΓΓ
ΓΓ
Ήέ…œΥυ ωΘΚ![]() Μρ
Μρ![]() ΓΘ
ΓΘ
ΓΑΒψΨΠΓ±±ΨΧβΩΦ≤ιΝΥ’ΐΖΫ–ΈΒΡ–‘÷ ΓΔΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΓΔ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ”κ≈–Ε®Β»÷Σ ΕΘ§ΩΦ≤ιΝΥΖ÷άύΧ÷¬έΒΡΥΦœκΘ§ΩΦ≤ιΝΥάϊ”ΟΜυ±ΨΜνΕ·Ψ≠―ιΫβΨωΈ ΧβΒΡΡήΝΠΘ§ΉέΚœ–‘Ζ«≥Θ«ΩΘ° λœΛ’ΐΖΫ–Έ”κ“ΜΗωΕ» ΐΈΣ45ΓψΒΡΫ«Ήι≥…ΒΡΜυ±ΨΆΦ–ΈΘ®Τδ÷–Ϋ«ΒΡΕΞΒψ”κ’ΐΖΫ–ΈΒΡ“ΜΗωΕΞΒψ÷ΊΚœΘ§Ϋ«ΒΡΝΫ±Ώ”κ’ΐΖΫ–ΈΒΡΝΫ±ΏΖ÷±πœύΫΜΘ© «ΫβΨω±ΨΧβΒΡΙΊΦϋΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΝΫΗωΙ≤“ΜΗωΕΞΒψΒΡΒ»―ϋRtΓςABCΘ§RtΓςCEFΘ§ΓœABC=ΓœCEF=90ΓψΘ§Ν§Ϋ”AFΘ§M «AFΒΡ÷–ΒψΘ§Ν§Ϋ”MBΓΔMEΘ°
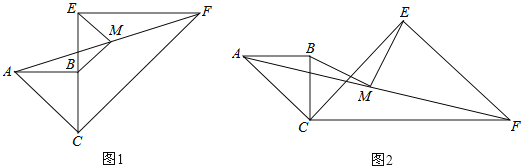
Θ®1Θ©»γΆΦ1Θ§Β±CB”κCE‘ΎΆ§“Μ÷±œΏ…œ ±Θ§«σ÷ΛΘΚMBΓΈCFΘΜ
Θ®2Θ©»γΆΦ1Θ§»τCB=aΘ§CE=2aΘ§«σBMΘ§MEΒΡ≥ΛΘΜ
Θ®3Θ©»γΆΦ2Θ§Β±ΓœBCE=45Γψ ±Θ§«σ÷ΛΘΚBM=MEΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«κ¥σΦ“‘ΡΕΝœ¬ΟφΝΫΕΈ≤ΡΝœΘ§≤ΔΫβ¥πΈ ΧβΘΚ
≤ΡΝœ1ΘΚΈ“Ο«÷ΣΒά‘Ύ ΐ÷α…œ±μ Ψ4ΚΆ1ΒΡΝΫΒψ÷°ΦδΒΡΨύάκΈΣ3Θ®»γΆΦ1Θ©Θ§Εχ|4©¹1|ΘΫ3Θ§Υυ“‘‘Ύ ΐ÷α…œ±μ Ψ4ΚΆ1ΒΡΝΫΒψ÷°ΦδΒΡΨύάκΈΣ|4©¹1|Θ°
≤ΡΝœ2ΘΚ‘Ό»γ‘Ύ ΐ÷α…œ±μ Ψ4ΚΆ©¹2ΒΡΝΫΒψ÷°ΦδΒΡΨύάκΈΣ6Θ®»γΆΦ2Θ©Εχ|4©¹Θ®©¹2Θ©|ΘΫ6Θ§Υυ“‘ ΐ÷α…œ±μ Ψ ΐ4ΚΆ©¹2ΒΡΝΫΒψ÷°ΦδΒΡΨύάκ|4©¹Θ®©¹2Θ©|Θ°
Θ®1Θ©Θ®»γΆΦ3Θ©ΗυΨί…œ ωΙφ¬…Θ§Έ“Ο«Ω…“‘ΒΟ≥ωΫα¬έΘΚ‘Ύ ΐ÷α…œ±μ Ψ ΐaΚΆ ΐbΝΫΒψ÷°ΦδΒΡΨύάκΒ»”ΎΓΓ ΓΓΘ°
Θ®2Θ© ‘“Μ ‘Θ§«σ‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐ5![]() ”κ©¹4
”κ©¹4![]() ΒΡΝΫΒψ÷°ΦδΒΡΨύάκΈΣΓΓ ΓΓΘ°
ΒΡΝΫΒψ÷°ΦδΒΡΨύάκΈΣΓΓ ΓΓΘ°
Θ®3Θ©“―÷Σ ΐ÷α…œ±μ Ψ ΐaΒΡΒψM”κ±μ Ψ ΐ©¹1ΒΡΒψ÷°ΦδΒΡΨύάκΈΣ3Θ§±μ Ψ ΐbΒΡΒψN”κ±μ Ψ ΐ2ΒΡΒψ÷°ΦδΒΡΨύάκΈΣ4Θ§«σMΘ§NΝΫΒψ÷°ΦδΒΡΨύάκΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΧθΕΪΈςΉΏœρΒΡ…Χ“ΒΫ÷…œΘ§“ά¥Έ”– ιΒξΘ®Φ«ΈΣAΘ©ΓΔάδ“ϊΒξΘ®Φ«ΈΣBΘ©ΓΔ–§ΒξΘ®Φ«ΈΣCΘ©Θ§άδ“ϊΒξΈΜ”Ύ–§ΒξΈς±Ώ50m¥ΠΘ§–§ΒξΈΜ”Ύ ιΒξΕΪ±Ώ60m¥ΠΘ§ΆθΤΫœ»»Ξ ιΒξΘ§»ΜΚσ―ΊΉ≈’βΧθΫ÷œρΕΪΉΏΝΥ30m÷ΝD¥ΠΘ§Ϋ”Ή≈œρΈςΉΏ50mΒΫ¥οE¥ΠΘ°
Θ®1Θ©“‘AΈΣ‘≠ΒψΓΔœρΕΪΈΣ’ΐΖΫœρΜ≠ ΐ÷αΘ§‘Ύ ΐ÷α…œ±μ Ψ≥ω…œ ωAΘ§BΘ§CΘ§DΘ§EΒΡΈΜ÷ΟΘΜ
Θ®2Θ©»τ‘Ύ’βΧθΫ÷…œΫ®“ΜΦ“≥§ –Θ§ Ι≥§ –”κ–§ΒξCΖ÷Ψ”EΒψΝΫ≤ύΘ§«“ΒΫEΒψΒΡΨύάκœύΒ»Θ§Έ ≥§ –‘Ύάδ“ϊΒξΒΡ ≤Ο¥ΖΫœρΘΩΨύάκΕύ‘ΕΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Χζ¬Ζ…œAΘ§BΝΫΒψœύΨύ25 kmΘ§CΘ§DΈΣΝΫ¥εΉ·Θ§DAΓΆAB”ΎΒψAΘ§CBΓΆAB”ΎΒψBΘ§“―÷ΣDAΘΫ15 kmΘ§CBΘΫ10 kmΘ§œ÷‘Ύ“Σ‘ΎΧζ¬ΖAB…œΫ®“ΜΗωΆΝΧΊ≤ζΤΖ ’ΙΚ’ΨEΘ§ ΙΒΟCΘ§DΝΫ¥εΒΫE’ΨΒΡΨύάκœύΒ»Θ§‘ρE’Ψ”ΠΫ®‘ΎάκA’ΨΕύ…Όkm¥ΠΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓθABCD÷–Θ§AEΤΫΖ÷ΓœBADΘ§ΫΜBC”ΎΒψEΘ§BFΤΫΖ÷ΓœABCΘ§ΫΜAD”ΎΒψFΘ§AE”κBFΫΜ”ΎΒψPΘ§Ν§Ϋ”EFΘ§PDΘ°

Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈABEF «Νβ–ΈΘΜ
Θ®2Θ©»τAB=4Θ§AD=6Θ§ΓœABC=60ΓψΘ§«σtanΓœDPFΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
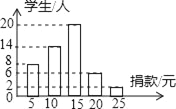
ΓΨΧβΡΩΓΩ‘Ύ“Μ¥ΈΨηΩνΜνΕ·÷–Θ§―ß–ΘΆ≈÷ß ιœκΝΥΫβ±Ψ–Θ―ß…ζΒΡΨηΩν«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ50Οϊ―ß…ζΒΡΨηΩνΫχ––ΝΥΆ≥ΦΤΘ§≤ΔΜφ÷Τ≥…»γΆΦΥυ ΨΒΡΆ≥ΦΤΆΦΘ°
Θ®1Θ©’β50ΟϊΆ§―ßΨηΩνΒΡ÷Ύ ΐΈΣΓΓ ΓΓ‘ΣΘ§÷–ΈΜ ΐΈΣΓΓ ΓΓ‘ΣΘΜ
Θ®2Θ©»γΙϊΨηΩνΒΡ―ß…ζ”–300»ΥΘ§ΙάΦΤ’β¥ΈΨηΩν”–Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ«λΉΘ‘ΣΒ©Θ§―ß–ΘΉΦ±ΗΨΌΑλ“Μ≥ΓΓΑΨ≠ΒδΥ–ΕΝΓ±ΜνΕ·Θ§Ρ≥ΑύΉΦ±ΗΆχΙΚ“Μ–©Ψ≠ΒδΥ–ΕΝ±ΨΚΆ ΨΕΝΙβ≈ΧΘ§Υ–ΕΝ±Ψ“ΜΧΉΕ®Φέ100‘ΣΘ§ ΨΕΝΙβ≈Χ“Μ’≈Ε®Φέ20‘ΣΘ°‘ΣΒ©ΤΎΦδΡ≥ΆχΒξΩΣ’Ι¥ΌœζΜνΕ·Θ§ΜνΕ·ΤΎΦδœρΩΆΜßΧαΙ©ΝΫ÷÷”≈ΜίΖΫΑΗΘΚ
ΖΫΑΗAΘΚ¬ρ“ΜΧΉΥ–ΕΝ±ΨΥΆ“Μ’≈ ΨΕΝΙβ≈ΧΘΜ
ΖΫΑΗBΘΚΥ–ΕΝ±ΨΚΆ ΨΕΝΙβ≈ΧΕΦΑ¥Ε®ΦέΒΡΨ≈’έΗΕΩνΘ°
œ÷Ρ≥ΑύΦΕ“Σ‘ΎΗΟΆχΒξΙΚ¬ρΥ–ΕΝ±Ψ10ΧΉΚΆ ΨΕΝΙβ≈Χx’≈Θ®xΘΨ10Θ©Θ§Ϋβ¥πœ¬Ν–»ΐΗωΈ ΧβΘΚ
Θ®1Θ©»τΑ¥ΖΫΑΗAΙΚ¬ρΘ§Ι≤–ηΗΕΩν ‘ΣΘ®”ΟΚ§xΒΡ ΫΉ”±μ ΨΘ©Θ§
»τΑ¥ΖΫΑΗBΙΚ¬ρΘ§Ι≤–ηΗΕΩν ‘ΣΘ®”ΟΚ§xΒΡ ΫΉ”±μ ΨΘ©ΘΜ
Θ®2Θ©»τ–ηΙΚ¬ρ ΨΕΝΙβ≈Χ15’≈Θ®Φ¥x=15Θ© ±Θ§«κΆ®ΙΐΦΤΥψΥΒΟςΑ¥ΡΡ÷÷ΖΫΑΗΙΚ¬ρΫœΈΣΚœΥψΘΜ
Θ®3Θ©»τ–ηΙΚ¬ρ ΨΕΝΙβ≈Χ15’≈Θ®Φ¥x=15Θ© ±Θ§ΡψΜΙΡήΗχ≥ω“Μ÷÷ΗϋΈΣ Γ«°ΒΡΙΚ¬ρΖΫΖ®¬πΘΩ»τΡήΘ§«κ–¥≥ωΡψΒΡΙΚ¬ρΖΫΖ®ΚΆΥυ–ηΖ―”ΟΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAΓΔBΝΫΒΊ‘Ύ ΐ÷α…œœύΨύ20ΟΉΘ§AΒΊ‘Ύ ΐ÷α…œ±μ ΨΒΡΒψΈΣ-8Θ§–ΓΈΎΙξ¥”AΒΊ≥ωΖΔ―Ί ΐ÷αΆυBΒΊΖΫœρ«ΑΫχΘ§ΒΎ“Μ¥Έ«ΑΫχ1ΟΉΘ§ΒΎΕΰ¥ΈΚσΆΥ2ΟΉΘ§ΒΎ»ΐ¥Έ‘Ό«ΑΫχ3ΟΉΘ§ΒΎΥΡ¥Έ”÷ΚσΆΥ4ΟΉΘ§Γ≠Γ≠Θ§Α¥¥ΥΙφ¬…––ΫχΘ§Θ® ΐ÷αΒΡ“ΜΗωΒΞΈΜ≥ΛΕ»Β»”Ύ1ΟΉΘ©
![]()
Θ®1Θ©«σBΒΊ‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐΘΜ
Θ®2Θ©»τBΒΊ‘Ύ‘≠ΒψΒΡΉσ≤ύΘ§Ψ≠ΙΐΒΎΈε¥Έ––ΫχΚσ–ΓΈΎΙξΒΫ¥οΒψPΘ§ΒΎΝυ¥Έ––ΫχΚσΒΫ¥οΒψQΘ§‘ρΒψPΚΆΒψQΒΫΒψAΒΡΨύάκœύΒ»¬πΘΩ«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τBΒΊ‘Ύ‘≠ΒψΒΡ”“≤ύΘ§Ρ«Ο¥Ψ≠Ιΐ30¥Έ––ΫχΚσΘ§–ΓΈΎΙξΒΫ¥οΒΡΒψ”κΒψB÷°ΦδΒΡΨύάκ «Εύ…ΌΟΉΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com