
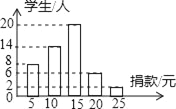
【题目】在一次捐款活动中,学校团支书想了解本校学生的捐款情况,随机抽取了50名学生的捐款进行了统计,并绘制成如图所示的统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)如果捐款的学生有300人,估计这次捐款有多少元?
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
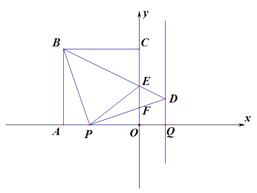
【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出![]() 关于直线x=-1对称的
关于直线x=-1对称的![]() ,并写出
,并写出![]() 各点坐标.
各点坐标.
(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 正方形OABC的边OA、OC在坐标轴上.在
正方形OABC的边OA、OC在坐标轴上.在![]() 轴上线段
轴上线段![]() (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为
(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为![]() .连接PB,过P作PB的垂线,过Q作
.连接PB,过P作PB的垂线,过Q作![]() 轴的垂线,两垂线相交于点D.连接BD交
轴的垂线,两垂线相交于点D.连接BD交![]() 轴于点E,连接PD交
轴于点E,连接PD交![]() 轴于点F,连接PE.
轴于点F,连接PE.
(1)求∠PBD的度数.
(2)设△POE的周长为![]() ,探索
,探索![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
(3)令![]() ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
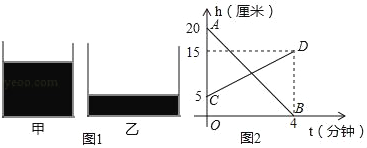
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
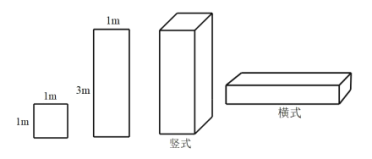
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
查看答案和解析>>
科目:初中数学 来源: 题型:
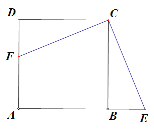
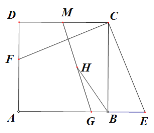
【题目】如图,四边形ABCD是正方形,在AB的延长线上取一点E,连接EC,过点C作CF⊥EC交AD于F.
(1)求证:EC=FC.
(2)若G、M分别是AB、CD上一动点,连接GM.H是GM上的中点,连接BH,当G、M运动到某一特殊位置时得到BH=BG +CM,此时∠ABH的度数是多少?请说明理由.
(3)在(2)的条件下,若BG=1,MC=![]() ,连接AH.求出四边形AHMD的面积.
,连接AH.求出四边形AHMD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180 ;③△EHF≌△DHC;④若![]() ,则3S△EDH=13S△DHC,其中结论正确的有___________.
,则3S△EDH=13S△DHC,其中结论正确的有___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com