
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.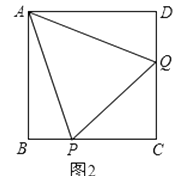
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 . 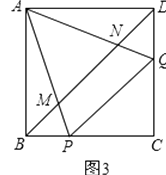
【答案】
(1)BF.,AED.
(2)解:将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
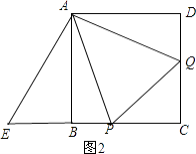
则∠D=∠ABE=90°,
即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵ 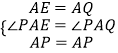 ,
,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ.
(3)
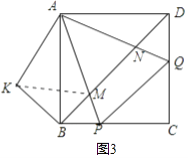
解:四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
【解析】(1)如图1,∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED.
(1)如图1,直接根据旋转的性质得到DE=BF,∠AFB=∠AED.
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,
则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ.
(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证△AMN≌△AMK,得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等量代换即可得到BM2+DN2=MN2.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生对A《最强大脑》、B《朗读者》、C《中国诗词大会》、D《出彩中国人》四个电视节目的喜爱情况,随机抽取了m学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),将调查结果绘制成如下两幅不完整的统计图(如图1和图2):
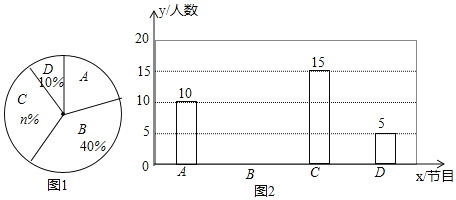
根据统计图提供的信息,回答下列问题;
(1)m= ,n= ;
(2)扇形统计图中,喜爱《最强大脑》节目所对应的扇形的圆心角度数是 度.
(3)根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查结果,请你估计该校6000名学生中有多少学生最喜欢《中国诗词大会》节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为18?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式维的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(﹣1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(﹣2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第124次跳动至A124的坐标( )

A.(63,62)B.(62,61)C.(﹣62,61)D.(124,123)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(﹣2,1),B(﹣1,4).
(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向上平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DBC的面积等于3,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网格中每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的格点上.

(1)将四边形ABCD进行平移,使点A移动到点D的位置,得到四边形DB′C′D′,画出平移后的图形;
(2)根据(1)所画的图形,请指出图中平行的线段;
(3)在(1)的基础上,若∠BDC=65°,求∠B′D′C′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.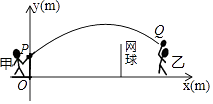
(1)当a=﹣ ![]() 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )

A. 5≤a≤12B. 12≤a≤3![]()
C. 12≤a≤4![]() D. 12≤a≤13
D. 12≤a≤13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com