
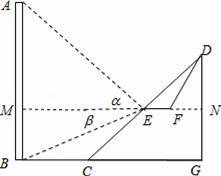
��ͼ����36��¥��AB������б��CD����E��б��CD���е㴦����֪б�µ��½ǣ�����DCG��Ϊ30�㣬AB��BC��
��1������A��B��C��D��E��G��ͬһ��ƽ���ڣ��ӵ�E�����¥��A�����Ǧ�Ϊ37�㣬¥��B�ĸ��Ǧ�Ϊ24�㣬�ʵ�A��E֮��ľ���AE�������ף�����ȷ��ʮ��λ��
��2���ּƻ���б���е�E����ȥ����б�£���һ��ƽ����ˮƽ��BC��ƽ̨EF��һ���µ�б��DF��ʹ��б��DF���±�Ϊ
 ��1��ijʩ���ӳн���������Ϊ��������������������֣�ʵ�ʹ���Ч����ߵ�ԭ�ƻ���1.5���������ԭ�ƻ���ǰ2���������ʩ����ԭ�ƻ�ƽ��ÿ���������ף�
��1��ijʩ���ӳн���������Ϊ��������������������֣�ʵ�ʹ���Ч����ߵ�ԭ�ƻ���1.5���������ԭ�ƻ���ǰ2���������ʩ����ԭ�ƻ�ƽ��ÿ���������ף�
���ο����ݣ�cos37���0.80��tan37���0.75��tan24���0.45��cos24���0.91��


�����㡿��ֱ�������ε�Ӧ��-�¶��½����⣻��ʽ���̵�Ӧ�ã���ֱ�������ε�Ӧ��-���Ǹ������⣮
����������1���ӳ�FE��AB��M����ME=x������ֱ�������κ����ó�AM=tan��•x��BM=tan��•x��Ȼ�����tan��•x+tan��•x=36���������EM�ij���Ȼ��ͨ�����Һ����������AE��
��2������BM=NG=DN���õ�DN�ij���Ȼ���ֱ�������κ������EN��FN���������EF��DF�ij���Ȼ����������г����̣��ⷽ�̼�����ã�
����𡿽⣺��1���ӳ�FE��AB��M��
��EF��BC��
��MN��AB��MN��DG��
��ME=x��
��AM=tan��•x��BM=tan��•x��
��AB=36��
��tan��•x+tan��•x=36��
��tan37��x+tan24��x=36��
0.75x+0.45x=36��
���x=30��
��AE=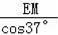
 =
=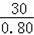
 ��37.5���ף���
��37.5���ף���
��2���ӳ�EF��DG��N��
��GN=BM=tan24��•30=13.5��DE=CE��EF��BC��
��DN=GN=13.5���ף���
�ߡ�DCG=30�㣬
���DEN=30�㣬
��EN=DN•cot30��=13.5��
 ��
��
��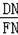
 =
=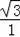
 ��
��
���DFN=60�㣬
���EDF=30�㣬FN=DN•cot60��=13.5��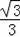
 ��
��
��DF=EF=EN��FN=13.5��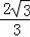
 ��
��
��EF+DF=27��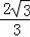
 =18
=18
 ��
��
��ʩ����ԭ�ƻ�ƽ��ÿ����y�ף�
��������ã�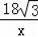
 =
=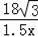
 +2��
+2��
���x=3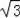
 ���ף���
���ף���
�����飬�Ƿ��̵ĸ���
��ʩ����ԭ�ƻ�ƽ��ÿ����3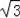
 �ף�
�ף�

�����������⿼���˽�ֱ�������ε�Ӧ�ã���Ŀ���漰���������Ǻ��¶Ƚǵ����⣬����Ĺؼ��ǹ���ֱ�������Σ�
��


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������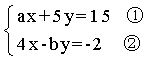 ���ڼ����˷��̢��е�a�õ��ķ�����Ľ�Ϊ
���ڼ����˷��̢��е�a�õ��ķ�����Ľ�Ϊ �ҿ����˷��̢��е�b���õ�������Ľ�Ϊ
�ҿ����˷��̢��е�b���õ�������Ľ�Ϊ ������ȷ��a��bΪ���㣬��ԭ������Ľ�x��y�IJ
������ȷ��a��bΪ���㣬��ԭ������Ľ�x��y�IJ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��a��b��0�������и�ʽ��һ����ȷ���ǣ� ��
A��a��b B��ab��0 C�� D����a����b
D����a����b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ�˽���������Ů��ѧ�����ijУ�����꼶���༶��������Ů���������������ͳ�ƣ����ָ��༶����������Ů��������1����2����3����4����5����6����������������Ƴ���������ͳ��ͼ��
��1�����У���꼶ƽ��ÿ���༶�ж�������������Ů������������ͳ��ͼ����������
��2��ѧУ������ֻ��2����������Ů����Щ�༶�У���ѡ�����������������������б�������״ͼ�ķ����������ѡ������������Ů����ͬһ���༶�ĸ��ʣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ʮ�˽��й������죩����Ͷ����ȫ��ɹ����ϣ����칲ǩԼ528����Ŀ��ǩԼ���602 000 000 000Ԫ��������602 000 000 000�ÿ�ѧ��������ʾΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������ֽƬABCD��AB=3��AD=5���۵�ֽƬ��ʹ��A����BC���ϵ�E�����ۺ�ΪPQ������E��BC�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���������P��Q�ֱ���AB��AD�����ƶ������E��BC���Ͽ��ƶ���������Ϊ��������


A��1 B��2 C��4 D��5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com