
分析 (1)分子、分母上下同乘$\sqrt{7}-\sqrt{6}$,即可解答;
(2)分子、分母上下同乘$\sqrt{n+1}-\sqrt{n}$,即可解答;
(3)利用(2)的规律,即可解答.
解答 解:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}=\frac{\sqrt{7}-\sqrt{6}}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}=\sqrt{7}-\sqrt{6}$.
(2)$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$.
(3)$\frac{1}{{\sqrt{2}+1}}$+$\frac{1}{{\sqrt{3}+\sqrt{2}}}$+$\frac{1}{{2+\sqrt{3}}}$+…+$\frac{1}{\sqrt{2011}+\sqrt{2010}}$
=$\sqrt{2}-1+\sqrt{3}-\sqrt{2}+2-\sqrt{3}+…+\sqrt{2011}$-$\sqrt{2010}$
=-1$+\sqrt{2011}$.
点评 本题考查分母有理化,解决本题的关键是根据分母有理化,发现规律.


科目:初中数学 来源: 题型:解答题
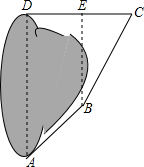 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一天大批产品的次品率情况 | B. | 了解某市初中生体育中考的成绩 | ||
| C. | 了解某城市居民的人均收入情况 | D. | 了解某一天离开某市的人口数量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 3 | 4 | x |
| -2 | y | a |
| 2y-x | c | b |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com