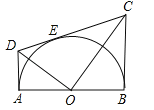
【题目】如图，AB为半圆O的在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③
，④OD：OC=DE：EC，⑤
，正确的有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
试题连接OE，如图所示：∵AD与圆O相切，DC与圆O相切，BC与圆O相切，∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB，AD∥BC，∴CD=DE+EC=AD+BC，选项②正确；
在Rt△ADO和Rt△EDO中，∵OD=OD，DA=DE，∴Rt△ADO≌Rt△EDO（HL），∴∠AOD=∠EOD，同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC，又∠AOD+∠DOE+∠EOC+∠COB=180°，∴2（∠DOE+∠EOC）=180°，即∠DOC=90°，选项①正确；
∴∠DOC=∠DEO=90°，又∠EDO=∠ODC，∴△EDO∽△ODC，∴
，即
，选项⑤正确；
∵∠AOD+∠COB=∠AOD+∠ADO=90°，∠A=∠B=90°，∴△AOD∽△BOC，∴
，选项③正确；
同理△ODE∽△OEC，∴
，选项④正确；
故选D．
科目：初中数学 来源： 题型：
【题目】已知二次函数
．
（1）求出该函数图象的顶点坐标，对称轴，图象与
轴、
轴的交点坐标；
（2）在什么范围内时，随的增大而增大？当在什么范围内时，随的增大而减小？
（3）当在什么范围内时，
？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线
经过第一、二、四象限，点
在上．
（1）在图中标出点
；
（2）若
，且过点
，求直线的解析式；
（3）在（2）的条件下，直接写出当
时，
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
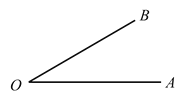
【题目】已知：∠AOB．
求作：∠A'O'B'，使∠A'O'B'=∠AOB．
作法：①以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
②画一条射线O'A'，以点O'为圆心，OC长为半径面弧，交O'A'于点C；
③以点C'为圆心，CD长为半径画弧，与第②步中所画的弧相交于点D'；
④过点D'画射线O'B’,则∠A'O'B'=∠AOB．
根据上面的作法，完成以下问题：
(1)使用直尺和圆规，作出∠A'O'B'(请保留作图痕迹)．
(2)完成下面证明∠A'O'B'=∠AOB的过程(注：括号里填写推理的依据)．
证明：由作法可知O'C'=OC，O'D'=OD，D'C'=_________，
∴△C'O'D'≌△COD(________)
∴∠A'O'B'=∠AOB(________)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一项工程，甲，乙两公司合做，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．
（1）甲，乙两公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司的施工费较少？
查看答案和解析>>
科目：初中数学 来源： 题型：
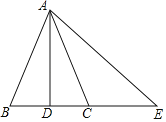
【题目】如图，在△ABC中，AB=AC，D是BC的中点，连接AD，E在BC的延长线上，连接AE，∠E=2∠CAD，下列结论：
①AD⊥BC；
②∠E=∠BAC；
③CE=2CD；
④AE=BE．
其中正确的个数是（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
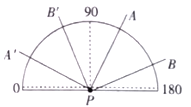
【题目】如图，把
放置在量角器上，
与量角器的中心重合，读得射线
、
分别经过刻度
和
，把绕点逆时针方向旋转到
，下列结论：
①
；
②若射线
经过刻度
，则
与
互补；
③若
，则射线经过刻度45．
其中正确的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△CDE的顶点C点坐标为C（1，﹣2），点D的横坐标为
，将△CDE绕点C旋转到△CBO，点D的对应点B在x轴的另一个交点为点A．
（1）图中，∠OCE等于∠_____；
（2）求抛物线的解析式；
（3）抛物线上是否存在点P，使S△PAE=
S△CDE？若存在，直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品的进价为每件
元．当售价为每件
元时，每星期可卖出
件，现需降价处理，为占有市场份额，且经市场调查：每降价
元，每星期可多卖出
件．现在要使利润为
元，每件商品应降价（ ）元．
A. 3 B. 2.5 C. 2 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com