练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

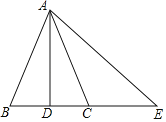
    【题目】如图，在△ABC中，AB=AC，D是BC的中点，连接AD，E在BC的延长线上，连接AE，∠E=2∠CAD，下列结论：

    ①AD⊥BC；

    ②∠E=∠BAC；

    ③CE=2CD；

    ④AE=BE．

    其中正确的个数是（　　）

    A.1个B.2个C.3个D.4个

    【答案】C

    【解析】

    等腰三角形的性质，“三线合一”，顶角的平分线，底边的高和底边上的中线，三条线互相重合便可推得.

    解：①∵在△ABC中，AB=AC，D是BC的中点，

    ∴AD⊥BC；

    ②∵在△ABC中，AB=AC，D是BC的中点，

    ∴∠BAC=2∠CAD，

    ∵∠E=2∠CAD，

    ∴∠E=∠BAC；

    ③无法证明CE=2CD；

    ④∵在中，AB=AC，

    ∴∠B=∠ACB，

    ∵∠ACB=∠E+∠CAE，∠E=∠BAC，

    ∴∠B=∠EAB，

    ∴AE=BE．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一家用电器开发公司研制出一种新型电子产品，每件的生产成本为元，按定价元出售，每月可销售万件．为了增加销量，公司决定采取降价的办法，经市场调研，每降价元，月销售量可增加万件．

    （1）求出月销售量（万件）与销售单价（元）之间的函数关系式（不必写的取值范围）；

    （2）求出月销售利润（万元）（利润售价-成本价）与销售单价（元）之间的函数关系式（不必写的取值范围）；

    （3）请你通过（2）中的函数关系式及其大致图象帮助公司确定产品的销售单价范围，使月销售利润不低于万元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，DB∥AC，且DB=AC，E是AC的中点，

    （1）求证：BC=DE；

    （2）连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标中，反比例函数y=（x＞0）的图象经过点A（1，4），B（a，b），其中a＞1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连接AD，DC，CB．

    （1）求k的值；

    （2）求证：DC∥AB；

    （3）当AD∥BC时，求直线AB的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为半圆O的在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③，④OD：OC=DE：EC，⑤，正确的有（ ）

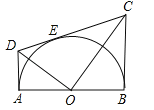
    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

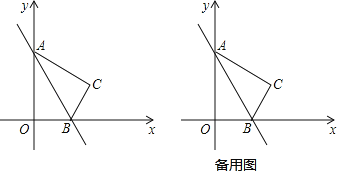
    【题目】如图，在坐标平面内，点O是坐标原点，A（0，6），B（2，0），且∠OBA=60°，将△OAB沿直线AB翻折，得到△CAB，点O与点C对应．

    （1）求点C的坐标：

    （2）动点P从点O出发，以2个单位长度/秒的速度沿线段OA向终点A运动，设△POB的面积为S（S≠0），点P的运动时间为t秒，求S与t的关系式，并直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某家电商场计划用9万元从生产厂家购进50台电视机，已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．

    （1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你计算一下商场有哪几种进货方案？

    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，应选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列游戏对双方公平的是（ ）

    A. 随意转动被等分成个扇形，且分别均匀涂有红、黄、绿三种颜色的转盘，若指针指向绿色区域，则小明胜，否则小亮胜

    B. 从一个装有个红球，个黄球和个黑球（这些球除颜色外完全相同）的袋中任意摸出一个球，若是红球，则小明胜，否则小亮胜

    C. 投掷一枚均匀的正方体形状的骰子，若偶数点朝上，则小明胜，若是奇数点朝上，则小亮胜

    D. 从分别标有数，，，，的五张纸条中，任意抽取一张，若抽到的纸条所标的数字为偶数，则小明胜，若抽到的纸条所标的数字为奇数，则小亮胜

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为参加学校艺术节闭幕演出，八年级一班欲租用男、女演出服装若干套以供演出时使用，已知4套男装和6套女装租用一天共需租金490元，6套男装和10套女装租用一天共需790元．

    （1）租用男装、女装一天的价格分别是多少？

    （2）由于演出时间错开租用高峰时段，男装、女装一天的租金分别给予9折和8折优惠，若该班演出团由5名男生和12名女生组成，求在演出当天该班租用服装实际支付的租金是多少？

    查看答案和解析>>

    同步练习册答案