
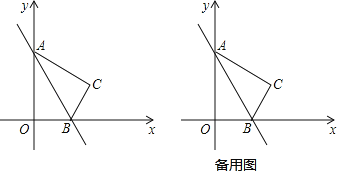
【题目】如图,在坐标平面内,点O是坐标原点,A(0,6),B(2![]() ,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
(1)求点C的坐标:
(2)动点P从点O出发,以2个单位长度/秒的速度沿线段OA向终点A运动,设△POB的面积为S(S≠0),点P的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围.
科目:初中数学 来源: 题型:
【题目】图甲和图乙分别是A,B两家酒店去年下半年的月营业额(单位:百万元)统计图.
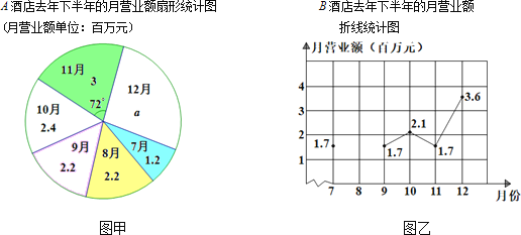
(1)求A酒店12月份的营业额a的值.
(2)已知B酒店去年下半年的月平均营业额为2.3百万元,求8月份的月营业额,并补全折线统计图.
(3)完成下面的表格(单位:百万元)
![]()
(4)综合以上分析,你认为哪一些数据更能较为准确的反映酒店的经营业绩?你认为哪家酒店的经营状况较好?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
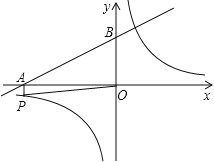
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,点P是AB上一动点,点Q是AC的延长线上一动点,且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同,PQ与BC相交于点D,若AB=![]() ,BC=16.
,BC=16.
(1)如图1,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,设BE+CD=λ,λ是否为常数?若是请求出λ的值,若不是请说明理由.
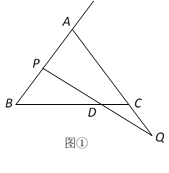
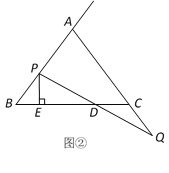
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,连接AD,E在BC的延长线上,连接AE,∠E=2∠CAD,下列结论:
①AD⊥BC;
②∠E=∠BAC;
③CE=2CD;
④AE=BE.
其中正确的个数是( )
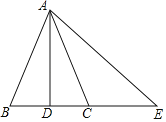
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快200m,两人同时从起点同向出发,经过3min两人首次相遇,此时乙还需跑150m才能跑完第一圈.
![]() 求甲、乙两人的速度分别是每分钟多少米?
求甲、乙两人的速度分别是每分钟多少米?![]() 列方程或者方程组解答
列方程或者方程组解答![]()
![]() 若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过
若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过![]() 两人再次相遇,则乙的速度至少要提高每分钟多少米?
两人再次相遇,则乙的速度至少要提高每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,我边防局通过雷达发现近海处有一可疑船只![]() 正向公海方向行驶,边防局迅速派出快艇
正向公海方向行驶,边防局迅速派出快艇![]() 追赶(图1).图2中
追赶(图1).图2中![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.
(分)之间的关系.
根据图象回答问题:

(1)哪一条线表示![]() 到海岸的距离与追赶时间的关系;
到海岸的距离与追赶时间的关系;
(2)求出![]() 的函数关系式;
的函数关系式;
(3)根据国际惯例,当![]() 船行驶到离海岸
船行驶到离海岸![]() 海里的公海时,将无法对其进行检查,照此速度,快艇
海里的公海时,将无法对其进行检查,照此速度,快艇![]() 能否在
能否在![]() 船驶入公海前将其拦截?
船驶入公海前将其拦截?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A.①②③B.②③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 8 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com